Смешанный ANOVA в R

Предположим, у нас есть данные вида:

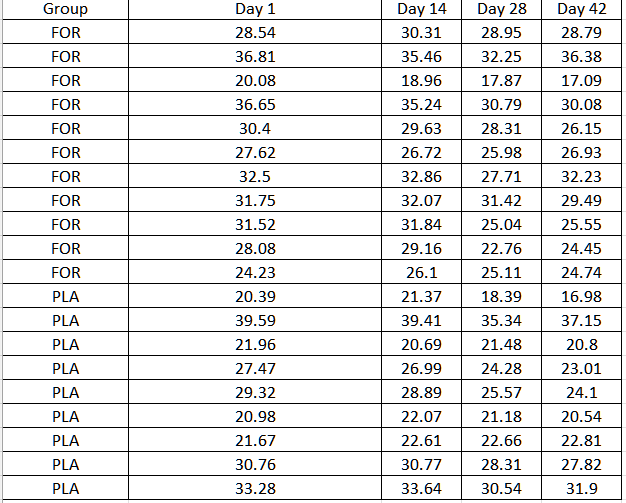
И мы хотели бы знать, был ли эффект взаимодействия группы, времени или группы и времени.

Сначала мы считываем данные и преобразуем их в длинный формат:

библиотека(openxlsx)

библиотека(lme4)
библиотека(afex) # для p-значений

библиотека(ggplot2)
библиотека(gtsummary)# для красивых таблиц

1TP4Прочитайте данные (укажите здесь путь к вашему файлу)
data.rep<-read.xlsx ("C:/Users/mmura/OneDrive/Dokumenty/FB/data.xlsx")

head(data.rep)
dim(data.rep)

1TP4Сделайте данные в длинном формате, добавив некоторые идентификаторы для отдельных лиц

data.long<-as.data.frame(cbind(ID=rep(seq(1:20),4),time=rep(c(1,14,28,42),each=20),
          resp=c(data.rep$Day.1,data.rep$Day.14,data.rep$Day.28,data.rep$Day.42),
          group=rep(data.rep$Group,4))
head(data.long)

data.long$time<-as.numeric(data.long$time)
data.long$resp<-as.numeric(data.long$resp)

В то же время мы добавляем некоторую идентификационную переменную для отдельных особей. Это могут быть пластины/измерения или то, что было измерено в изменяющихся условиях.

В качестве следующего шага мы сделаем некоторую визуализацию:

1TP4Сделайте визуализацию

1TP4Индивидуальные профили
ggplot(data.long, aes(x=time, y=resp,color=ID)) + geom_smooth()+geom_point()+
  ylab("Ваш ответ")+xlab("Время (дни)")

1TP4Теперь линейные данные по ID
ggplot(data.long, aes(x=time, y=resp,color=ID)) + geom_smooth(method = "lm",se=FALSE)+geom_point()+
  ylab("Ваш ответ")+xlab("Время (дни)")

1TP4Из этого мы делаем вывод о включении случайных наклонов

1TP4Сглаженные по группам
ggplot(data.long, aes(x=time, y=resp,color=group)) + geom_smooth()+geom_point()+
  ylab("Ваш ответ")+xlab("Время (дни)")

1TP4Теперь линейный график по группам
ggplot(data.long, aes(x=time, y=resp,color=group)) + geom_smooth(method = "lm",se=FALSE)+geom_point()+
  ylab("Ваш ответ")+xlab("Время")

Ниже представлены только линейные графики:

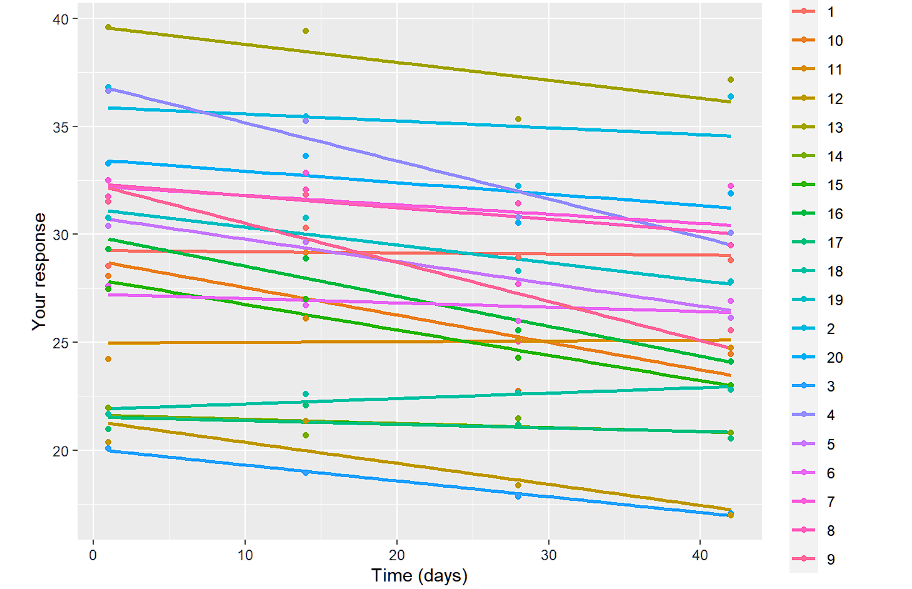
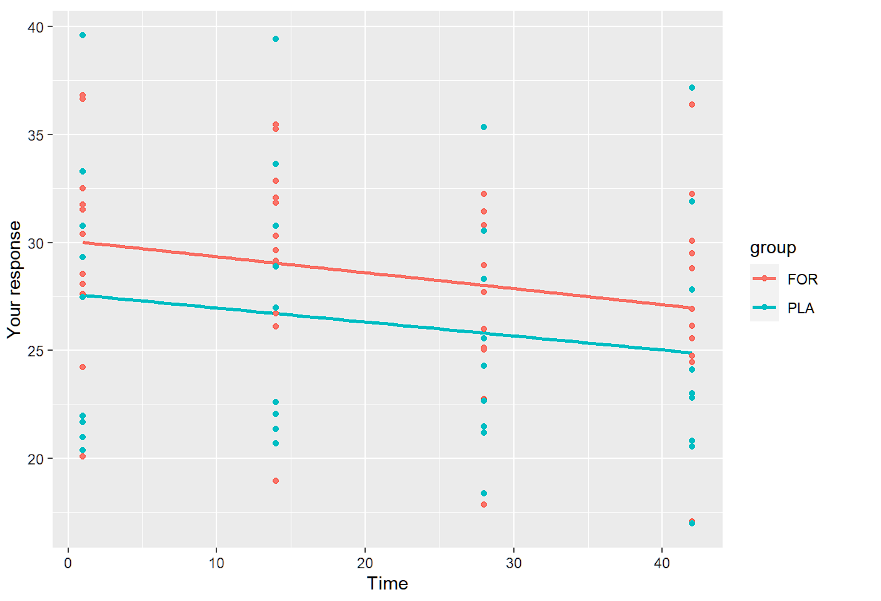
Цель этих визуализаций - понять, нужны ли нам случайные перехват и наклон и является ли линейная модель правильной в первую очередь. Кроме того, рассматривая профили по группам, мы видим, чего следует ожидать. Профили параллельны, поэтому эффект "группа*время" не будет значительным.

Затем мы подгоняем исходную модель:

1TP4Подгонка модели
m.initial<-lmer(resp~time*group+(1+time|ID),data=data.long)
summary(m.initial)
tbl_regression(m.final)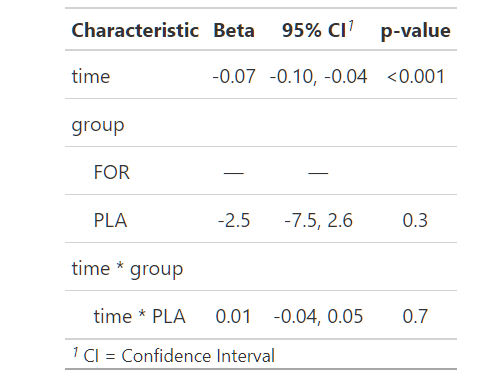

Поскольку эффект взаимодействия не является значимым, мы удаляем его из модели:

1TP4Поскольку группа*время не является значимой, мы исключаем ее

m.2<-lmer(resp~time+group+(1+time|ID),data=data.long)
summary(m.2)

Эффект основной группы также не является значимым. Поэтому в окончательной модели будет только фиксированный эффект времени:

m.final<-lmer(resp~time+(1+time|ID),data=data.long)
summary(m.final)


tbl_regression(m.final)

Таким образом, окончательный вывод таков:

Эффект отрицательной тенденции значим в итоговой смешанной модели. В среднем с каждым днем отклик уменьшается на 0,07 единицы.

Итоговый файл RMD имеет следующий вид Вот.

А данные Вот.