R 中的混合方差分析

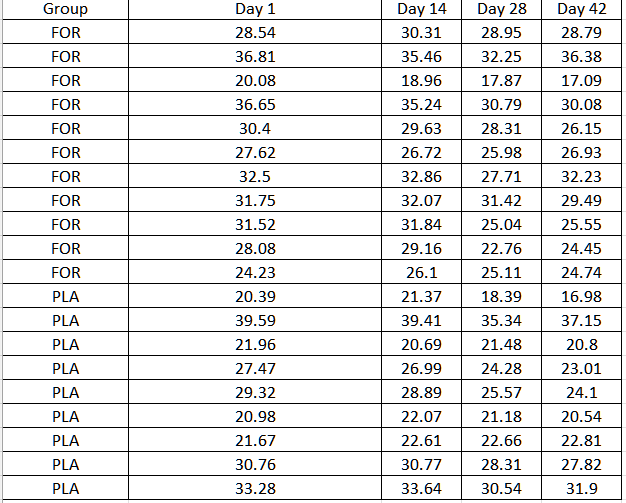
假设我们有这样一个数据

我们还想知道是否存在组别、时间或组别*时间的交互效应。

首先，我们读取数据并将其转换为长格式：

library(openxlsx)

library(lme4)
library(afex) # for p-values

函数库（ggplot2）
库（gtsummary）# 用于漂亮的表格

#read 数据（在此输入文件路径）
data.rep<-read.xlsx ("C:/Users/mmura/OneDrive/Dokumenty/FB/data.xlsx")

head(data.rep)
dim(data.rep)

1TP4制作长格式数据，为个人添加一些 ID

data.long<-as.data.frame(cbind(ID=rep(seq(1:20),4),time=rep(c(1,14,28,42),each=20)、
          resp=c(data.rep$Day.1,data.rep$Day.14,data.rep$Day.28,data.rep$Day.42)、
          group=rep(data.rep$Group,4))
head(data.long)

data.long$time<-as.numeric(data.long$time)
data.long$resp<-as.numeric(data.long$resp)

同时，我们还要为个体添加一些 ID 变量。这可以是板块/措施或在变化条件下测量的任何东西。

下一步，我们要做一些可视化工作：

# 做一些可视化

1TP4个人概况
ggplot(data.long, aes(x=time, y=resp,color=ID))+ geom_smooth()+geom_point()+
  ylab("Your response")+xlab("Time (days)")

#now ID 线性
ggplot(data.long, aes(x=time, y=resp,color=ID))+ geom_smooth(method = "lm",se=FALSE)+geom_point()+
  ylab("您的回复")+xlab("时间（天数）")

#由此我们得出结论，也应包括随机斜率

# 按组平滑
ggplot(data.long, aes(x=time, y=resp,color=group))+ geom_smooth()+geom_point()+
  ylab("Your response")+xlab("Time (days)")

#now 线性分组
ggplot(data.long, aes(x=time, y=resp,color=group))+ geom_smooth(method = "lm",se=FALSE)+geom_point()+
  ylab("您的回复")+xlab("时间")

下面我们只展示线性图：

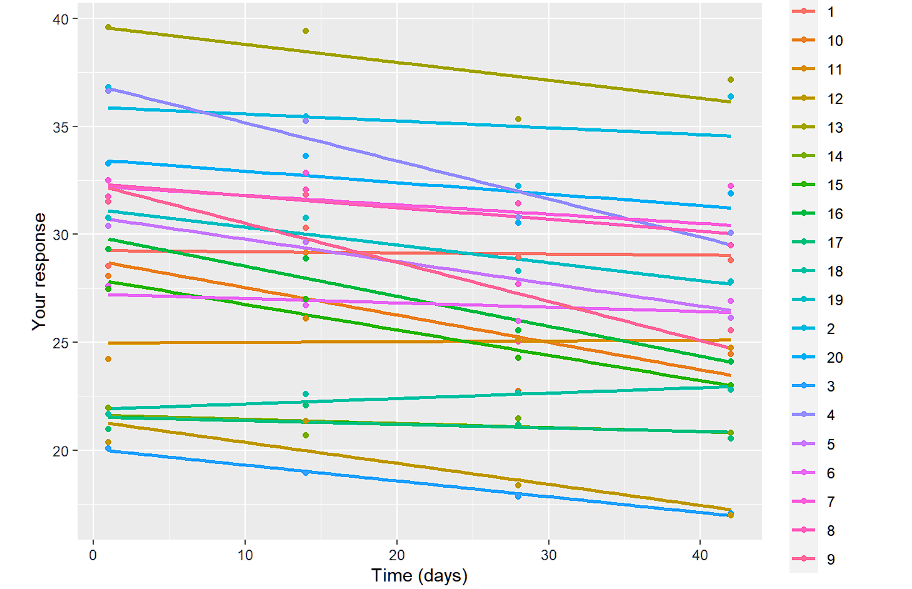
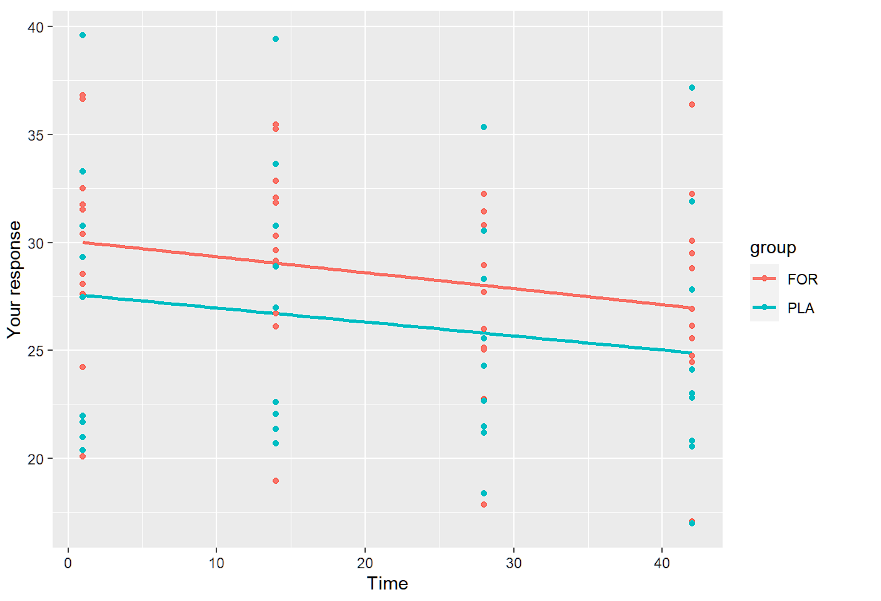
这些可视化的目的是了解我们是否需要随机截距和斜率，以及线性模型是否是正确的模型。此外，通过检查各组的剖面图，我们还可以看到预期的结果。剖面图是平行的，因此组*时间效应并不显著。

然后，我们对初始模型进行拟合：

# 拟合模型
m.initial<-lmer(resp~time*group+(1+time|ID),data=data.long)
summary(m.initial)
tbl_regression(m.final)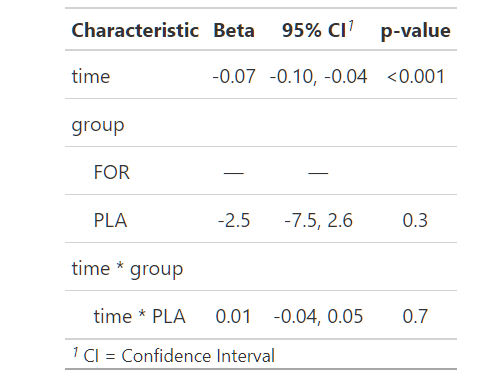

由于交互效应不显著，我们将其从模型中删除：

#S由于组别*时间不显著，我们将其排除在外

m.2<-lmer(resp~time+group+(1+time|ID),data=data.long)
summary(m.2)

主要群体效应也不显著。因此，在最终模型中只有固定时间效应：

m.final<-lmer(resp~time+(1+time|ID),data=data.long)
summary(m.final)


tbl_regression(m.final)

因此，最终结论如下：

在最终的混合模型中，负趋势效应非常明显。平均每一天，响应都会减少 0.07 个单位。

最终的 RMD 文件是 这里.

数据是 这里。