ROC-кривая - то, что вы всегда хотели знать, но боялись спросить...

Этот пост, как и многие другие, навеян вопросом студента. Оказывается, многие из нас используют ROC-кривые в анализе, не совсем понимая, для чего эти кривые нужны и как они создаются.

Модели классификации стали очень популярным инструментом и являются частью многих внедренных широко доступных решений "черного ящика", часто как часть инструментов машинного обучения. С одной стороны, такая легкая доступность готовых к использованию инструментов очень заманчива и побуждает людей пробовать их. С другой стороны, поскольку все уже дано, никто не стремится получить дополнительные знания о методе. Очень часто не видно реализованного кода таких моделей классификации. Поэтому неясно, что скрывается за этим черным ящиком.

Возьмем пример из медицины. Предположим, что у нас есть двоичный ответ 0-1, обозначающий, болен ли пациент (1) или здоров (0). Кроме того, у нас есть некоторые данные о пациентах, которые, как мы думаем или знаем, могут быть потенциальными предикторами вероятности быть больным или здоровым, например, возраст, индекс массы тела, пол или курение. Модель, которая связывает наш бинарный предиктор с заданной линейной комбинацией предикторов, называется моделью логистической регрессии. Она является обобщением хорошо известной линейной нормальной регрессионной модели, но на этот раз наш ответ является бинарным, а не непрерывным, и нам нужно связать этот бинарный ответ с линейной частью модели. Это происходит с помощью так называемой функции связи, которая представляет собой функцию логита для модели логистической регрессии. В R код для подгонки модели логистической регрессии выглядит следующим образом:

my_model<-glm(binary_response~ age + smoke + bmi + gender,family=binomial, data=my_data))
summary(my_model)

Приведенная выше модель может быть окончательной моделью после применения некоторой процедуры построения по частям для получения окончательного набора значимых предикторов. Или мы можем захотеть проверить эти предикторы на наших данных, зная из литературы, что они были признаны значимыми в других исследованиях.

Обратите внимание, что мы строим модели по двум причинам:

1. Для умозаключений, чтобы сделать выводы. Затем мы действительно должны устранить эти не значимые предикаты, используя, например, некоторую процедуру обратного исключения.
2. Для целей прогнозирования. Тогда модель может быть перегружена. Нам не так важно, что в ней находится, лишь бы она обладала хорошей предсказательной способностью.

Давайте сосредоточимся на второй цели, потому что именно здесь пригодится кривая ROC. Но сначала о главном. После подгонки модели мы хотим увидеть, насколько хорош прогноз, сделанный с помощью этой модели. В идеале, мы должны построить/обучить нашу модель на так называемых обучающий набор а затем проверить его на другом испытательный комплект. Это могут быть одни и те же данные, но мы просто используем часть из них в качестве обучающей части, а другую часть - в качестве тестирующей. Возникает вопрос, в какой пропорции мы должны это делать. Это нетривиальный вопрос, и он является предметом так называемого перекрестная валидация методы. В идеале мы должны исследовать различные расщепления и повторить эту процедуру путем случайной выборки из наших данных. Пока предположим, что у нас были экспериментальные данные, которые использовались для построения модели, а теперь у нас есть новые данные, для которых мы хотим проверить эффективность нашей модели.

Сначала мы создаем прогнозы нашего ответа на основе подогнанной логистической модели.

predicted<-predict(my_model,type=c("response"))

Важно понимать, что прогнозируется вероятность, а не двоичный ответ. Допустим, для пациента X прогноз составил 0,7. Значит ли это, что он/она болен? Ну, если мы предположим, что все, у кого вероятность >0,5, больны, то да, он/она больны в соответствии с нашей моделью. Выбор порог 0,5 здесь имеет решающее значение. После того, как мы выбрали, например, 0,5, мы можем исследовать производительность модели.

predicted.threshold  my_threshold)

Если мы выберем my_treshold равным 0,5, то ответ precited.treshold будет бинарным. Он будет равен 1 для тех вероятностей >0,5 и 0 в противном случае. Затем мы можем посмотреть на матрицу путаницы.

table(my_data$binary_response,predicted.threshold)

предсказанный.порог
    
      0 1
  0 25 304
  1 13 258

Из этой матрицы путаницы мы можем увидеть, сколько ложноположительный результат (ЛП) Наблюдения, которые у нас есть, - это те, кого модель предсказала как больных (1), но они оказались здоровыми. Кроме того, мы будем иметь ложноотрицательный (FN) наблюдений, то есть те, которые прогнозировались как здоровые, но на самом деле оказались больными. Остальные наблюдения будут истинно положительные результаты (ИП)правильно спрогнозированы как больные и истинные негативы (TN), правильно спрогнозированы как здоровые.

Общим показателем для оценки эффективности модели является чувствительность=ТП/Пэто доля всех больных пациентов (P), выявленных как больные. Второй мерой является так называемый специфичность=TN/Nэто доля всех здоровых пациентов, признанных здоровыми.

Теперь никто не говорит нам, что наш порог должен быть 0,5. Почему не 0,6? Если мы изменим порог, предсказания изменятся, матрица путаницы изменится, а чувствительность и специфичность изменятся.

Как выбрать этот порог, чтобы максимизировать специфичность и чувствительность? Идея заключается в том, чтобы они оба были высокими. Но если чувствительность повышается, то специфичность снижается, и наоборот. Это компромисс между этими двумя параметрами.

Так нужно ли нам запускать код для всех этих возможных порогов? Нет, кривая ROC сделает это за нас.

library(pROC)

myROC<- roc(my_data$binary_response ~ predicted)

plot(myROC)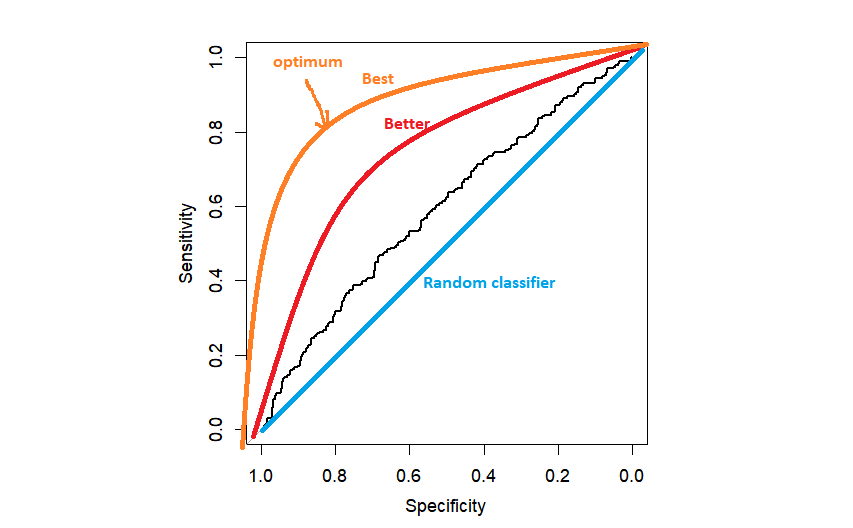

На практике мы можем получить нечто похожее на черную кривую ROC, только немного лучше, чем случайный классификатор. Чем ближе к левому верхнему углу находится ROC, тем лучше, потому что мы ближе к максимальной специфичности=1 и максимальной чувствительности=1.

Следующий вопрос как выбрать порог. Наиболее популярным методом является выбор порога, который максимизирует расстояние до левого верхнего угла. Это может быть сделано автоматически с помощью R, но полезно один раз запрограммировать это самостоятельно.

topleft<-(1-myROC$sensitivities)^2+(1-myROC$specificities)^2
topleft.threshold<-which(topleft==min(topleft))
text(x=myROC$specificities[topleft.threshold], y=myROC$sensitivities[topleft.threshold],"(0.50,0.58)",col=2)

Как только мы нашли оптимальную точку, мы можем нанести ее на график с помощью текстовой функции. На этом моменте обычно останавливаются, сообщая, наконец, AUC (площадь под кривой) как общую предсказательную способность модели. Но мы не должны останавливаться на этом. Мы хотим выяснить, какой порог (точка отсечения) соответствует оптимальной точке чувствительности и специфичности.

# для заданной чувствительности и специфичности
idx.which<-which((myROC$specificities==0.50)&(myROC$sensitivities==0.58))

1TP4Теперь мы берем порог
myROC$thresholds[idx.which]

predict.treshold  myROC$thresholds[idx.which])
Матрица #confusion
table(my_data$binary_response,predict.threshold)

Теперь мы нашли оптимальный порог myROC$thresholds[idx.which] и можем использовать его для сокращения наших предсказанных вероятностей.

Как я уже говорил, площадь под ROC-кривой обычно используется в качестве критерия для подведения итогов общей предсказательной способности нашей модели. Важно понимать, что это способность по всем возможным порогам. Чем ближе к 1, тем лучше. AUC для случайного классификатора равен 0,5, что соответствует площади под диагональной линией на графике выше.

Модели классификации - это, конечно, гораздо большее семейство, чем просто модели логистической регрессии. Это широкая тема исследования. Полезно знать, что существуют и другие методы, помимо "левого верхнего угла" для выбора оптимального критерия, например, критерий Жудена. В этом критерии чувствительность и специфичность считаются одинаково важными. Но это не всегда так. Нужно смотреть на конкретные данные, потому что ваша настройка может быть совершенно иной, чем в чьем-то другом учебнике. Возвращаясь к примеру с медициной. Если ваша болезнь - рак, вы больше беспокоитесь о ложноотрицательных наблюдениях, чем о ложноположительных. Эти ложноположительные результаты будут в дальнейшем диагностированы, но пропуск некоторых пациентов с раком может привести к их смерти. В таких условиях вы скорее максимизируете чувствительность за счет специфичности. С другой стороны, если ваша болезнь - ВИЧ, вы, вероятно, одинаково обеспокоены как ложноотрицательными, так и ложноположительными пациентами.

Удачи с вашими моделями!