منحنى ROC - ما أردت دائمًا معرفته ولكنك كنت تخشى أن تسأل عنه...

هذا المنشور مستوحى من سؤال الطالب، كما هو حال الكثير منها. يبدو أن الكثيرين منا يستخدمون منحنيات ROC في التحليل دون أن يعرفوا حقًا ما هي هذه المنحنيات وكيف يتم إنشاؤها.

لقد أصبحت نماذج التصنيف أداة شائعة جدًا وهي جزء من العديد من حلول الصندوق الأسود المتاحة على نطاق واسع، وغالبًا ما تكون جزءًا من أدوات التعلم الآلي. فمن ناحية، يعد هذا التوافر السهل للأدوات الجاهزة للاستخدام مغريًا للغاية ويشجع الناس على تجربتها. ومن ناحية أخرى، بما أنها معطاة، فلا أحد يسعى إلى معرفة إضافية حول الطريقة. في كثير من الأحيان لا يرى المرء الكود المنفذ لنماذج التصنيف هذه. لذلك، ليس من الواضح ما الذي يختبئ وراء هذا الصندوق الأسود.

لنأخذ مثالاً من الطب. لنفترض أن لدينا إجابة ثنائية من 0-1، تشير إلى ما إذا كان المريض مريضاً (1) أو سليماً (0). بالإضافة إلى ذلك، لدينا بعض البيانات عن المرضى التي نعتقد أو نعرف أنها قد تكون متنبئات محتملة لاحتمال أن يكون المريض مريضاً أو سليماً، مثل العمر أو مؤشر كتلة الجسم أو الجنس أو التدخين. يُطلق على النموذج الذي يربط بين متنبئنا الثنائي والمجموعة الخطية من المتنبئات نموذج الانحدار اللوجستي. وهو تعميم لنموذج الانحدار الطبيعي الخطي المعروف، لكن هذه المرة تكون استجابتنا ثنائية وليست متصلة ونحتاج إلى ربط هذه الاستجابة الثنائية بالجزء الخطي من النموذج. يحدث ذلك عبر ما يسمى بدالة الارتباط، وهي دالة لوغاريتمية لنموذج الانحدار اللوجستي. في لغة R، تكون شيفرة ملاءمة نموذج الانحدار اللوجستي كما يلي:

my_model<-glm(binary_response~ عمر ~ دخان + دخان + bmi + جنس، عائلة=بينومي، بيانات=my_data))
ملخص(my_model)

قد يكون النموذج المذكور أعلاه نموذجاً نهائياً بعد تطبيق بعض إجراءات البناء التجزيئي للحصول على المجموعة النهائية من المتنبئات المهمة. أو قد نرغب في اختبار هذه المتنبئات على بياناتنا مع العلم من الأدبيات أنها وُجدت مهمة في دراسات أخرى.

لاحظ أننا نبني النماذج لسببين:

1. للاستدلال، لدفع الاستنتاجات. ثم يجب علينا حقًا استبعاد تلك التنبؤات غير المهمة باستخدام بعض إجراءات الاستبعاد العكسي على سبيل المثال.
2. لغرض التنبؤ. ثم يمكن الإفراط في ضبط النموذج. لا نهتم كثيرًا بما هو موجود طالما أنه يتمتع بقدرة جيدة على التنبؤ.

دعونا نركز على هذا الغرض الثاني لأن هذا هو المكان الذي يكون فيه منحنى ROC مفيدًا. لكن أولاً وقبل كل شيء. بعد تركيب النموذج، نريد أن نرى مدى جودة التنبؤ من هذا النموذج. من الناحية المثالية، يجب أن نبني/ندرب نموذجنا على ما يسمى مجموعة التدريب ثم اختبره على الآخر مجموعة الاختبار. يمكن أن تكون البيانات نفسها ولكننا نستخدم جزءًا منها كجزء تدريبي وجزءًا آخر كجزء اختباري. السؤال الذي يطرح نفسه هو بأي نسبة يجب أن نفعل ذلك. الأمر ليس بديهياً وهو موضوع ما يسمى بـ التحقق التبادلي الطرق. من الناحية المثالية، يجب علينا فحص تقسيمات مختلفة وتكرار هذا الإجراء عن طريق أخذ عينات عشوائية من بياناتنا. في الوقت الحالي، لنفترض أن لدينا بياناتنا التجريبية التي استخدمناها لبناء نموذج، والآن لدينا بيانات جديدة نريد التحقق من أداء نموذجنا.

أولاً، نقوم بإنشاء تنبؤات لاستجابتنا من النموذج اللوجستي المجهز.

متوقع<-تنبؤ(my_model,type=c("استجابة"))

من المهم أن ندرك أنه سيكون الاحتمال الذي يتم التنبؤ به، وليس الاستجابة الثنائية. لنفترض أن التنبؤ بالنسبة للمريض X كان 0.7. هل هذا يعني أنه مريض؟ حسناً، إذا افترضنا أن كل شخص لديه احتمال > 0.5 مريض، فنعم، هو/هي مريض وفقاً لنموذجنا. اختيار العتبة 0.5 أمر حاسم هنا. بعد أن نختار على سبيل المثال 0.5 يمكننا فحص أداء النموذج.

العتبة المتوقعة  عتبتي)

إذا اخترنا أن تكون my_treshold 0.5، فستكون استجابة precited.treshold ثنائية. ستكون 1 لتلك الاحتمالات > 0.5 و 0 فيما عدا ذلك. يمكننا بعد ذلك النظر إلى مصفوفة الارتباك.

جدول (my_data$P4Tbinary_response,predicted.threshold)

العتبة المتوقعة
    
      0 1
  0 25 304
  1 13 258

من مصفوفة الالتباس هذه، يمكننا أن نرى كم عدد إيجابية كاذبة (FP) الملاحظات التي لدينا، وهي تلك التي تنبأ بها النموذج على أنها مريضة (1) ولكنها سليمة. بالإضافة إلى ذلك، سيكون لدينا سلبية كاذبة (ف ن) الملاحظات، وهي تلك التي تم التنبؤ بها على أنها سليمة، ولكنها في الواقع مريضة. أما بقية الملاحظات فستكون الإيجابيات الحقيقية (TP)تنبأت بشكل صحيح بأنها مريضة و السلبيات الحقيقية (ت.ن)تنبؤات صحيحة وصحيّة.

المقياس المشترك لتقييم أداء النموذج هو الحساسية=TP/Pوهي نسبة جميع المرضى (P) الذين تم اكتشاف إصابتهم بالمرض. المقياس الثاني هو ما يسمى الخصوصية=TN/N، وهي نسبة جميع المرضى الأصحاء الذين تم اكتشاف أنهم أصحاء.

الآن، لم يخبرنا أحد أن الحد الأدنى يجب أن يكون 0.5. لماذا ليس 0.6؟ إذا غيّرنا العتبة، ستتغير التنبؤات، وستتغير مصفوفة الارتباك وستتغير الحساسية والخصوصية.

كيف تختار هذه العتبة لزيادة الخصوصية والحساسية إلى أقصى حد؟ الفكرة هي أن يكون كلاهما مرتفعاً. ولكن بمجرد أن ترتفع الحساسية تنخفض الخصوصية والعكس صحيح. إنها مفاضلة بين هذين الأمرين.

إذن هل نحتاج إلى تشغيل الكود لكل هذه العتبات المحتملة؟ لا، فمنحنى ROC سيقوم بذلك نيابةً عنا.

مكتبة(pROC)

myROC<- roc(my_data$binary_response ~ متوقع)

رسم بياني(myROC)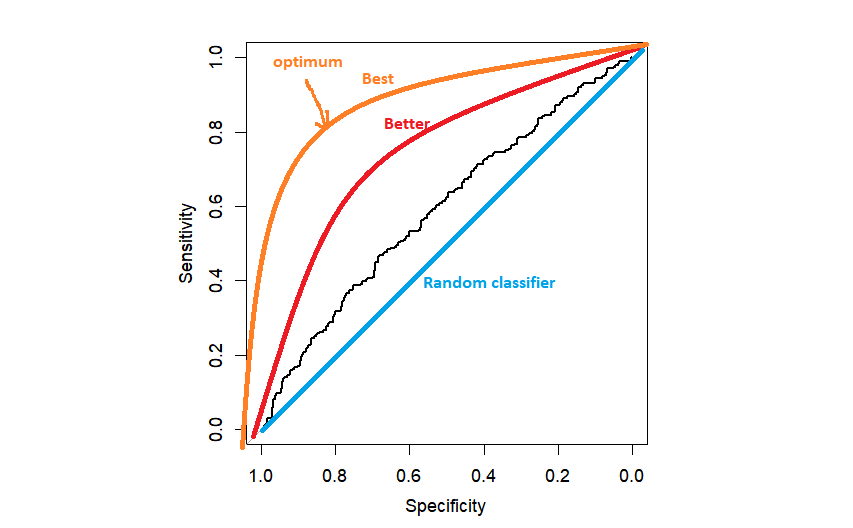

في الممارسة العملية، قد نحصل على شيء مثل منحنى ROC الأسود، أفضل قليلاً من المصنف العشوائي. كلما كان منحنى ROC أقرب إلى الزاوية العلوية اليسرى، كان ذلك أفضل لأننا نكون أقرب إلى الحد الأقصى للخصوصية=1 والحد الأقصى للحساسية=1.

السؤال التالي هو كيفية اختيار العتبة. الطريقة الأكثر شيوعًا هي اختيار العتبة التي تزيد من المسافة إلى الزاوية العلوية اليسرى. يمكن أن يتم ذلك تلقائيًا بواسطة R، ولكن من الجيد أن تبرمجه مرة واحدة بنفسك.

topleft<-(1-(1-ميROC$sensitivities)^2+(1-ميROC$specities)^2
topleft.threshold<-أي (topleft==دقيقة (topleft))
نص(x= myROC$sensitivities[topleft.threshold], y=myROC$sensitivities[topleft.threshold],"(0.50,0.58)",col=2)

بمجرد العثور على تلك النقطة المثلى يمكننا وضعها على الرسم البياني باستخدام الدالة النصية. عند هذه النقطة، عادةً ما يتوقف المرء عند هذه النقطة، ونقوم في النهاية بالإبلاغ عن AUC (المنطقة تحت المنحنى) باعتبارها القدرة التنبؤية الإجمالية للنموذج. لكن لا يجب أن نتوقف هنا. نريد معرفة العتبة (نقطة القطع) التي تتوافق مع نقطة الحساسية والخصوصية المثلى.

# لحساسية وخصوصية معينة
idx.which<-أيهما((myROC$specificities==0.50)&(myROC$sensitivities==0.58))

1TP5الآن نأخذ العتبة
myROC$P4Theresholds[idx.which]

predict.treshold  myROC$P4Tthresholds[idx.which])
مصفوفة #confusion
الجدول(my_data$Tbinary_response,predict.threshold)

لقد وجدنا الآن العتبة المثلى myROC$P4thresholds[idx.which] ويمكننا استخدامها لخفض الاحتمالات المتوقعة.

كما ذكرت من قبل، تُستخدم المساحة تحت منحنى ROC عادةً كمعيار لتلخيص القدرة الإجمالية للنموذج على التنبؤ. من الجيد أن ندرك أن هذه هي القدرة عبر جميع العتبات الممكنة. كلما كانت أقرب إلى 1، كان ذلك أفضل. AUC للمصنف العشوائي يساوي 0.5، وهو ما يتوافق مع المساحة تحت الخط القطري في الرسم البياني أعلاه.

نماذج التصنيف هي بالطبع عائلة أكبر بكثير من مجرد نماذج الانحدار اللوجستي. إنه موضوع واسع للبحث. من الجيد أن نعرف أن هناك طرقاً أخرى غير الزاوية "العلوية اليسرى" لاختيار المعيار الأمثل مثل معيار جودن. يعامل هذا المعيار الحساسية والخصوصية بنفس القدر من الأهمية. ولكن ليس هذا هو الحال دائمًا. يحتاج المرء إلى النظر إلى البيانات الخاصة التي بين أيدينا لأن قد يكون الإعداد الخاص بك مختلفًا تمامًا عن ذلك الموجود في البرنامج التعليمي لشخص آخر. بالعودة إلى المثال الطبي. إذا كان مرضك هو السرطان، فأنت قلق بشأن الملاحظات السلبية الكاذبة أكثر من الملاحظات الإيجابية الكاذبة. سيتم تشخيص تلك الإيجابيات الكاذبة بشكل أكبر ولكن قد يؤدي فقدان بعض مرضى السرطان إلى وفاتهم. في هذا الإعداد، ستفضل زيادة الحساسية إلى أقصى حد مقابل تكلفة الخصوصية. من ناحية أخرى، إذا كان مرضك هو فيروس نقص المناعة البشرية، فمن المحتمل أن تكون قلقًا بنفس القدر من كلا الأمرين، المرضى السلبيين الكاذبين والإيجابيين الكاذبين.

حظاً موفقاً مع نماذجك!