Mieszana ANOVA w R

Załóżmy, że mamy dane w postaci:

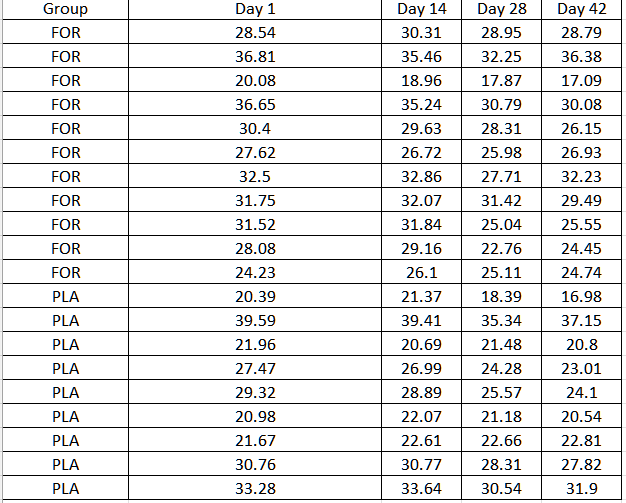
Chcielibyśmy też wiedzieć, czy wystąpił jakikolwiek efekt interakcji grupy, czasu lub grupy*czasu.

Najpierw odczytujemy dane i przekształcamy je w długi format:

library(openxlsx)

library(lme4)
library(afex) # dla wartości p

library(ggplot2)
library(gtsummary)# dla ładnych tabel

#read dane (umieść ścieżkę do pliku tutaj)
data.rep<-read.xlsx ("C:/Users/mmura/OneDrive/Dokumenty/FB/data.xlsx")

head(data.rep)
dim(data.rep)

#wórz dane w długim formacie, dodając identyfikatory dla poszczególnych osób

data.long<-as.data.frame(cbind(ID=rep(seq(1:20),4),time=rep(c(1,14,28,42),each=20),
          resp=c(data.rep$Day.1,data.rep$Day.14,data.rep$Day.28,data.rep$Day.42),
          group=rep(data.rep$Group,4)))
head(data.long)

data.long$time<-as.numeric(data.long$time)
data.long$resp<-as.numeric(data.long$resp)

Jednocześnie dodajemy zmienną identyfikacyjną dla poszczególnych osób. Mogą to być płytki/środki lub cokolwiek, co zostało zmierzone w zmieniających się warunkach.

Następnym krokiem jest wizualizacja:

1TP4Wykonaj wizualizację

#indywidualne profile
ggplot(data.long, aes(x=time, y=resp,color=ID)) + geom_smooth()+geom_point()+
  ylab("Twoja odpowiedź")+xlab("Czas (dni)")

#eraz liniowy według ID
ggplot(data.long, aes(x=time, y=resp,color=ID)) + geom_smooth(method = "lm",se=FALSE)+geom_point()+
  ylab("Twoja odpowiedź")+xlab("Czas (dni)")

#z tego wnioskujemy o uwzględnieniu również losowych nachyleń

#wygładzone przez grupę
ggplot(data.long, aes(x=time, y=resp,color=group)) + geom_smooth()+geom_point()+
  ylab("Twoja odpowiedź")+xlab("Czas (dni)")

#eraz liniowy według grupy
ggplot(data.long, aes(x=time, y=resp,color=group)) + geom_smooth(method = "lm",se=FALSE)+geom_point()+
  ylab("Twoja odpowiedź")+xlab("Czas")

Poniżej przedstawiamy tylko wykresy liniowe:

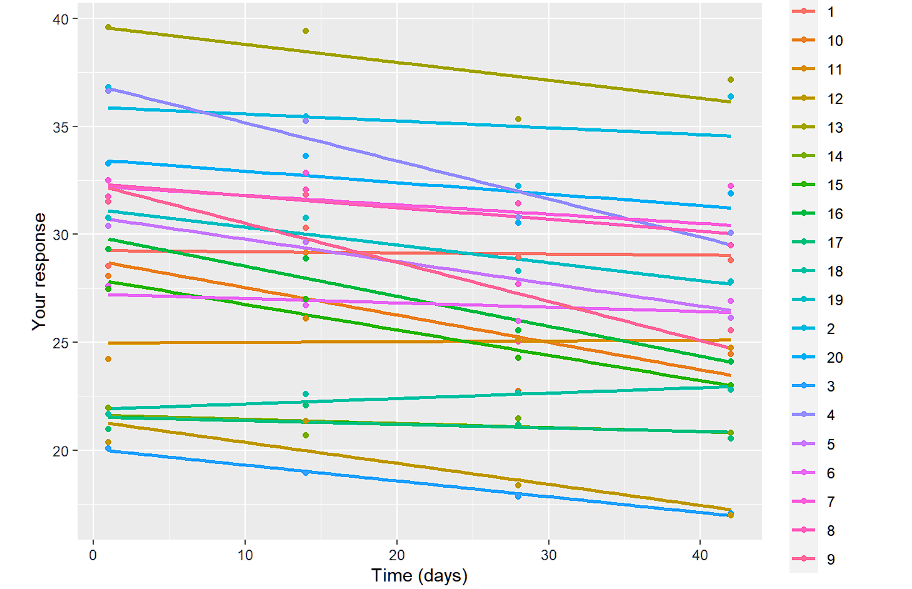
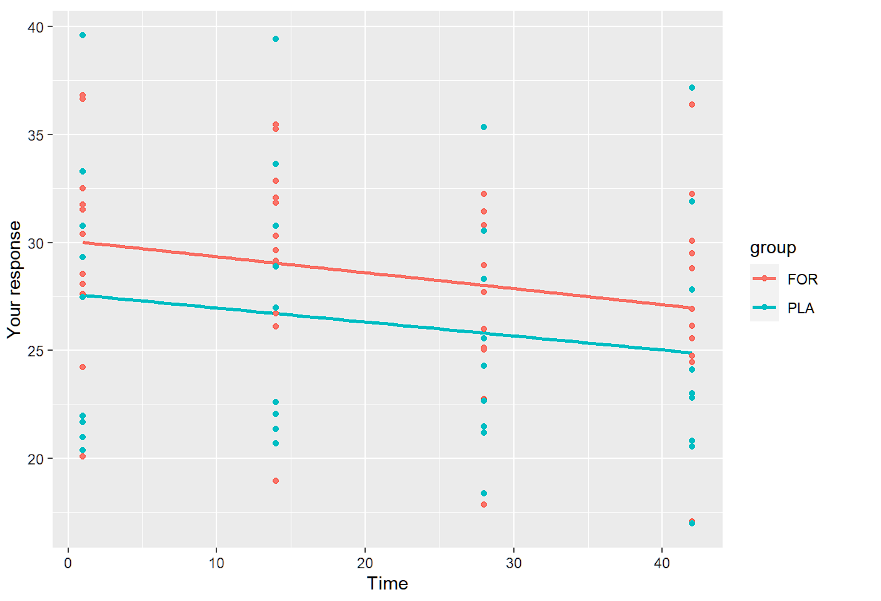
Celem tych wizualizacji jest sprawdzenie, czy potrzebujemy losowego punktu przecięcia i nachylenia oraz czy model liniowy wydaje się być właściwy. Ponadto, sprawdzając profile według grup, widzimy, czego się spodziewać. Profile są równoległe, więc efekt grupa*czas nie będzie znaczący.

Następnie dopasowujemy początkowy model:

1TP4Dopasowanie modelu
m.initial<-lmer(resp~time*group+(1+time|ID),data=data.long)
summary(m.initial)
tbl_regression(m.final)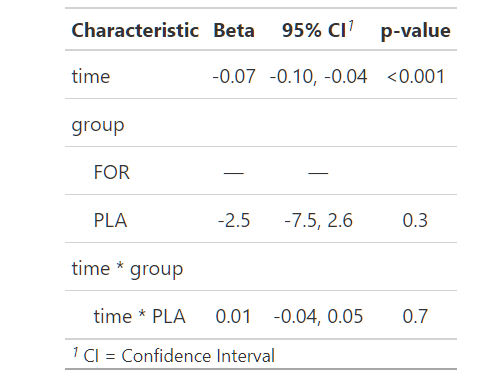

Ponieważ efekt interakcji nie jest znaczący, usuwamy go z modelu:

#S Ponieważ grupa*czas nie jest znacząca, wykluczamy ją

m.2<-lmer(resp~time+group+(1+time|ID),data=data.long)
summary(m.2)

Główny efekt grupowy również nie jest istotny. Dlatego w ostatecznym modelu będzie tylko stały efekt czasu:

m.final<-lmer(resp~time+(1+time|ID),data=data.long)
summary(m.final)


tbl_regression(m.final)

Dlatego ostateczny wniosek jest następujący:

Ujemny efekt trendu jest istotny w ostatecznym modelu mieszanym. Średnio z każdym dniem odpowiedź spada o 0,07 jednostki.

Ostateczny plik RMD to tutaj.

A dane są następujące tutaj.