Gemischte ANOVA in R

Angenommen, wir haben Daten der Form:

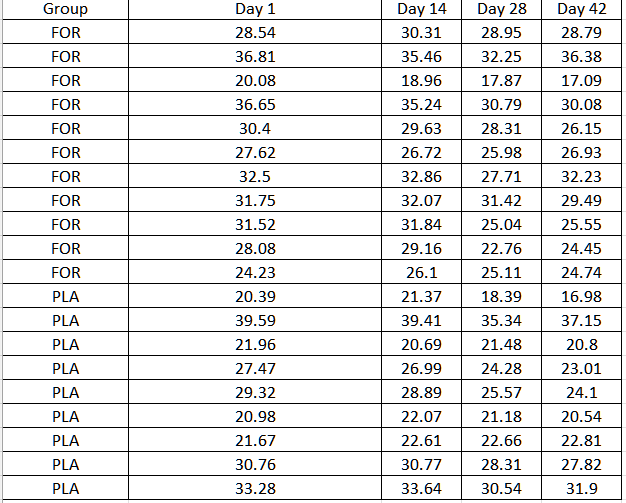
Und wir würden gerne wissen, ob es einen Interaktionseffekt zwischen Gruppe, Zeit oder Gruppe*Zeit gab.

Zunächst lesen wir die Daten und wandeln sie in ein Langformat um:

bibliothek(openxlsx)

bibliothek(lme4)
library(afex) #für p-Werte

bibliothek(ggplot2)
library(gtsummary)#für schöne Tabellen

#read the data (geben Sie hier den Pfad zu Ihrer Datei an)
data.rep<-read.xlsx ("C:/Users/mmura/OneDrive/Dokumenty/FB/data.xlsx")

head(daten.rep)
dim(daten.rep)

1TP4Erstellen von Daten in einem langen Format, Hinzufügen einer ID für Einzelpersonen

data.long<-as.data.frame(cbind(ID=rep(seq(1:20),4),time=rep(c(1,14,28,42),each=20),
          resp=c(data.rep$Day.1,data.rep$Day.14,data.rep$Day.28,data.rep$Day.42),
          group=rep(data.rep$Group,4)))
head(daten.lang)

data.long$time<-as.numeric(data.long$time)
daten.lang$resp<-as.numeric(daten.lang$resp)

Gleichzeitig fügen wir eine ID-Variable für Einzelpersonen hinzu. Dabei kann es sich um Platten/Messungen oder andere Dinge handeln, die unter den veränderten Bedingungen gemessen wurden.

Als nächsten Schritt führen wir eine Visualisierung durch:

1TP4Die Visualisierung

#einzelne Profile
ggplot(data.long, aes(x=time, y=resp,color=ID)) + geom_smooth()+geom_point()+
  ylab("Ihre Antwort")+xlab("Zeit (Tage)")

1TP4Nun das Lineare nach ID
ggplot(data.long, aes(x=time, y=resp,color=ID)) + geom_smooth(method = "lm",se=FALSE)+geom_point()+
  ylab("Ihre Antwort")+xlab("Zeit (Tage)")

#daraus lässt sich schließen, dass auch zufällige Steigungen einbezogen werden sollten

#geglättet nach Gruppe
ggplot(data.long, aes(x=time, y=resp,color=group)) + geom_smooth()+geom_point()+
  ylab("Ihre Antwort")+xlab("Zeit (Tage)")

1TP4Nun das Lineare nach Gruppe
ggplot(data.long, aes(x=time, y=resp,color=group)) + geom_smooth(method = "lm",se=FALSE)+geom_point()+
  ylab("Ihre Antwort")+xlab("Zeit")

Im Folgenden werden nur die linearen Diagramme gezeigt:

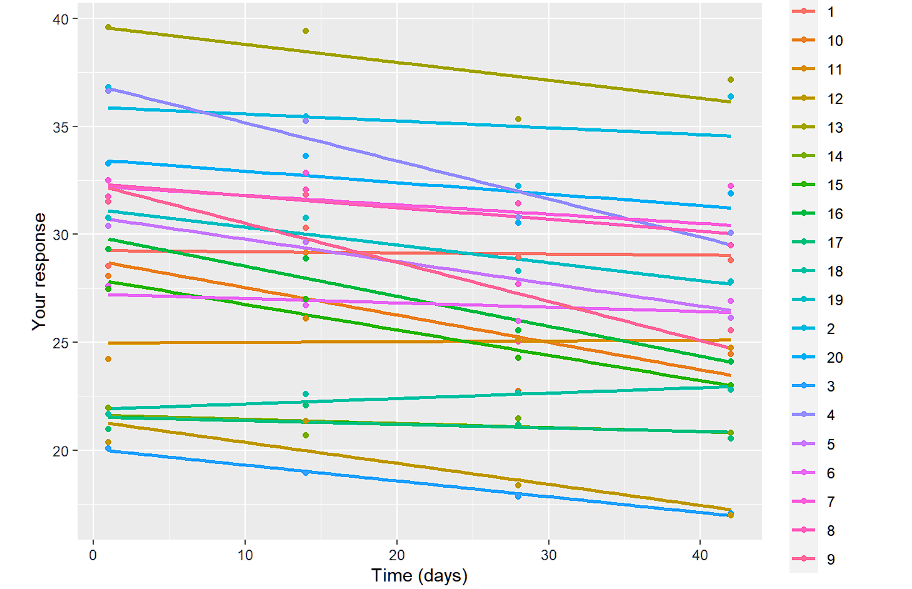
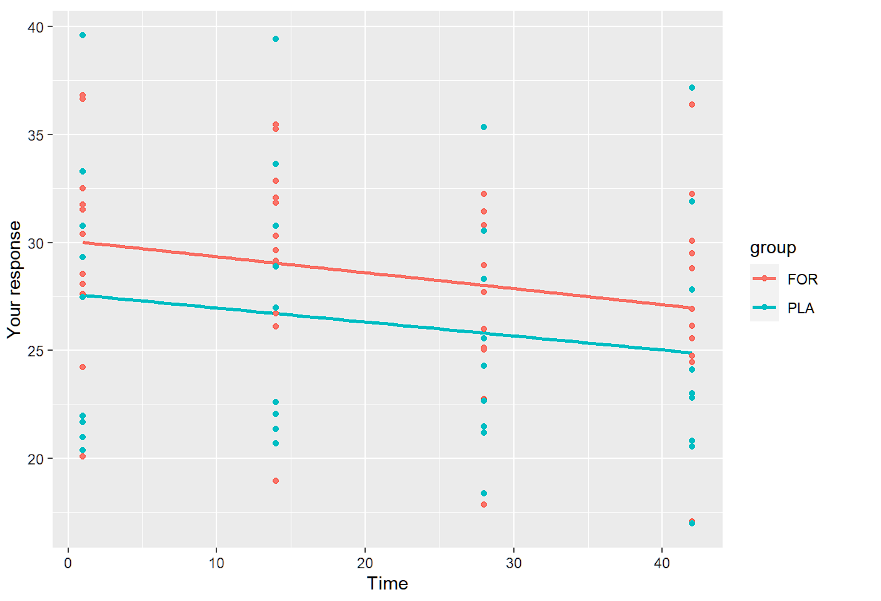
Der Zweck dieser Visualisierungen ist es, zu sehen, ob wir einen zufälligen Achsenabschnitt und eine zufällige Steigung benötigen und ob das lineare Modell überhaupt das richtige zu sein scheint. Durch die Inspektion der gruppenspezifischen Profile sehen wir auch, was zu erwarten ist. Die Profile sind parallel, so dass der Gruppe*Zeit-Effekt nicht signifikant sein wird.

Dann passen wir das ursprüngliche Modell an:

1TP4Anpassen eines Modells
m.initial<-lmer(resp~time*group+(1+time|ID),data=data.long)
Zusammenfassung(m.initial)
tbl_regression(m.final)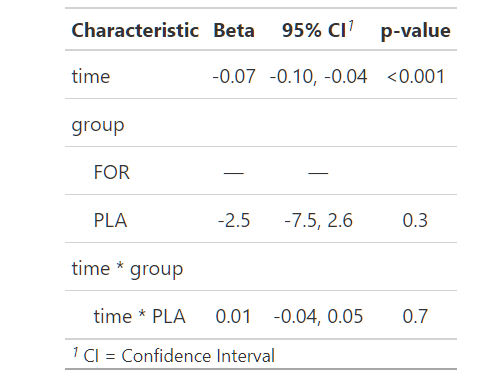

Da der Interaktionseffekt nicht signifikant ist, wird er aus dem Modell entfernt:

#SDa Gruppe*Zeit nicht signifikant ist, schließen wir sie aus.

m.2<-lmer(resp~time+group+(1+time|ID),data=data.long)
summary(m.2)

Der Hauptgruppeneffekt ist ebenfalls nicht signifikant. Daher wird im endgültigen Modell nur der feste Zeiteffekt berücksichtigt:

m.final<-lmer(resp~time+(1+time|ID),data=data.long)
Zusammenfassung(m.final)


tbl_regression(m.final)

Daher lautet die endgültige Schlussfolgerung wie folgt:

Der negative Trendeffekt ist in dem endgültigen gemischten Modell signifikant. Im Durchschnitt sinkt die Antwort mit jedem einzelnen Tag um 0,07 Einheiten.

Die endgültige RMD-Datei lautet Hier.

Und die Daten sind hier.