Krzywa ROC - co zawsze chciałeś wiedzieć, ale bałeś się zapytać...

Ten post jest inspirowany, jak wiele z nich, pytaniem studenta. Okazuje się, że wielu z nas wykorzystuje w analizie krzywe ROC nie do końca wiedząc do czego służą te krzywe i jak się je tworzy.

Modele klasyfikacyjne stały się bardzo popularnym narzędziem i są częścią wielu wdrożonych szeroko dostępnych rozwiązań typu black-box, często jako element narzędzi uczenia maszynowego. Z jednej strony ta łatwa dostępność gotowych narzędzi jest bardzo kusząca i zachęca ludzi do ich wypróbowania. Z drugiej strony, ponieważ jest podana, nikt nie szuka dodatkowej wiedzy o metodzie. Bardzo często nie widzi się zaimplementowanego kodu takich modeli klasyfikacyjnych. Dlatego nie wiadomo, co kryje się za tą czarną skrzynką.

Weźmy przykład z medycyny. Załóżmy, że mamy binarną odpowiedź 0-1, oznaczającą czy pacjent jest chory (1) czy zdrowy (0). Dodatkowo mamy pewne dane o pacjentach, które jak sądzimy lub wiemy mogą być potencjalnymi predyktorami prawdopodobieństwa bycia chorym lub zdrowym, takie jak wiek, BMI, płeć czy palenie. Model, który łączy nasz binarny predyktor ze zbiorem liniowych kombinacji predyktorów nazywa się modelem regresji logistycznej. Jest to uogólnienie dobrze znanego liniowego modelu regresji normalnej, ale tym razem nasza odpowiedź jest binarna, a nie ciągła i musimy połączyć tę binarną odpowiedź z liniową częścią modelu. Dzieje się to za pomocą tzw. funkcji łączącej, która jest funkcją logitową dla modelu regresji logistycznej. W R kod do dopasowania modelu regresji logistycznej jest następujący:

my_model<-glm(binary_response~ age + smoke + bmi + gender,family=binomial, data=my_data))
summary(my_model)

Powyższy model może być ostatecznym modelem po zastosowaniu pewnej procedury budowania w kawałkach, aby uzyskać ostateczny zestaw znaczących predyktorów. Albo możemy chcieć przetestować te predyktory na naszych danych, wiedząc z literatury, że zostały one uznane za istotne w innych badaniach.

Zauważ, że budujemy modele z dwóch powodów:

1. Do wnioskowania, do kierowania wnioskami. Wtedy rzeczywiście powinniśmy wyeliminować te nieistotne predyktory stosując np. jakąś procedurę eliminacji wstecznej.
2. Do celów predykcji. Wtedy model może być nadmiernie dopasowany. Nie zależy nam tak bardzo na tym, co jest w środku, dopóki ma dobrą zdolność predykcji.

Skupmy się na tym drugim celu, bo tam właśnie przydaje się krzywa ROC. Ale najpierw rzeczy pierwsze. Po dopasowaniu modelu chcemy zobaczyć jak dobra jest predykcja z tego modelu. Idealnie byłoby zbudować/przetrenować nasz model na tzw. zestaw szkoleniowy a następnie przetestować go na drugim zestaw testowy. Mogą to być te same dane, ale po prostu używamy ich części jako części treningowej, a innej części jako testowej. Powstaje pytanie, w jakich proporcjach powinniśmy to robić. Nie jest ono banalne i jest przedmiotem tzw. walidacja krzyżowa metody. W idealnym przypadku powinniśmy zbadać różne podziały i powtórzyć tę procedurę, losowo wybierając próbki z naszych danych. Na razie załóżmy, że mieliśmy nasze dane pilotażowe, które posłużyły do budowy modelu, a teraz mamy nowe dane, dla których chcemy sprawdzić działanie naszego modelu.

Najpierw tworzymy predykcje naszej odpowiedzi z dopasowanego modelu logistycznego.

predicted<-predict(my_model,type=c("response"))

Ważne jest, aby zdać sobie sprawę, że będzie to prawdopodobieństwo, które jest przewidywane, a nie odpowiedź binarna. Załóżmy, że dla pacjenta X przewidywanie wynosiło 0,7. Czy to oznacza, że jest on chory? Cóż, jeśli założymy, że każdy z prawdopodobieństwem >0,5 jest chory, to tak, jest chory według naszego modelu. Wybór próg 0,5 jest tutaj kluczowe. Po wybraniu np. 0,5 możemy zbadać wydajność modelu.

predicted.threshold  my_threshold)

Jeśli wybierzemy my_treshold na 0.5 to odpowiedź precited.treshold będzie binarna. Będzie ona wynosić 1 dla tych prawdopodobieństw >0,5 i 0 w przeciwnym wypadku. Następnie możemy spojrzeć na macierz konfuzji.

table(moje_dane$binary_response,predicted.threshold)

predicted.threshold
    
      0 1
  0 25 304
  1 13 258

Z tej macierzy konfuzji możemy zobaczyć, ile wynik fałszywie dodatni (FP) obserwacje, które mamy, czyli osoby przewidywane przez model jako chore (1), ale są zdrowe. Dodatkowo będziemy mieli. fałszywie negatywny (FN) obserwacje, czyli te, które są przewidywane jako zdrowe, a w rzeczywistości są chore. Pozostałe obserwacje to. wyniki prawdziwie pozytywne (TP), przewidywano prawidłowo jako chore i prawdziwe negatywy (TN), przewidywał prawidłowo jako zdrowy.

Wspólną miarą oceny wydajności modelu jest czułość=TP/P, czyli odsetek wszystkich chorych pacjentów (P) wykrytych jako chorych . Drugą miarą jest tzw. swoistość=TN/N, czyli odsetek wszystkich zdrowych pacjentów wykrytych jako zdrowi.

Teraz nikt nie mówi nam, że nasz próg musi wynosić 0,5. Dlaczego nie 0,6? Jeśli zmienimy próg, predykcje się zmienią, zmieni się macierz konfuzji i zmieni się czułość i specyficzność.

Jak wybrać ten próg, aby zmaksymalizować specyficzność i czułość? Chodzi o to, by oba były wysokie. Ale kiedy czułość idzie w górę, specyficzność idzie w dół i odwrotnie. Jest to kompromis pomiędzy tymi dwoma.

Czy musimy więc uruchomić kod dla wszystkich tych możliwych progów? Nie, krzywa ROC zrobi to za nas.

library(pROC)

myROC<- roc(my_data$binary_response ~ predicted)

plot(myROC)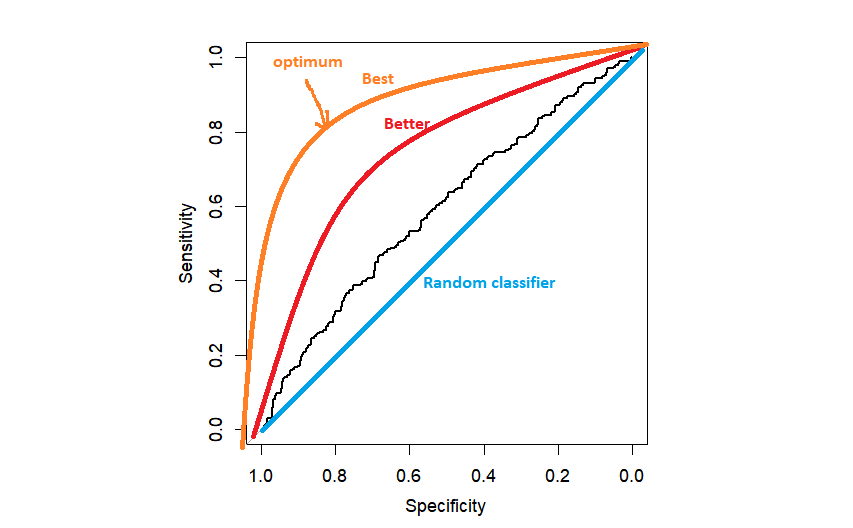

W praktyce możemy uzyskać coś takiego jak czarna krzywa ROC, tylko trochę lepiej niż losowy klasyfikator. Im bliżej lewego górnego rogu jest ROC, tym lepiej, ponieważ jesteśmy bliżej maksymalnej specyficzności=1 i maksymalnej czułości=1.

Kolejne pytanie to. jak wybrać próg. Najpopularniejszą metodą jest wybór progu, który maksymalizuje odległość od lewego górnego rogu. Może to być zrobione automatycznie przez R, ale dobrze jest zaprogramować to raz samodzielnie.

topleft<-(1-myROC$wrażliwości)^2+(1-myROC$specyficzności)^2
topleft.threshold<-which(topleft==min(topleft))
text(x=myROC$specificities[topleft.threshold], y=myROC$sensitivities[topleft.threshold],"(0.50,0.58)",col=2)

Gdy już znaleźliśmy ten optymalny punkt, możemy go umieścić na wykresie za pomocą funkcji tekstowej. W tym momencie zwykle się zatrzymuje, podając ostatecznie AUC (area under the curve) jako całkowitą zdolność predykcyjną modelu. Nie powinniśmy jednak na tym poprzestać. Chcemy dowiedzieć się, który próg (punkt odcięcia) odpowiada optymalnemu punktowi czułości i specyficzności.

# dla danej czułości i specyficzności
idx.which<-which((myROC$specificities==0.50)&(myROC$sensitivities==0.58))

#eraz bierzemy próg
myROC$thresholds[idx.which]

predict.treshold  myROC$thresholds[idx.which])
Macierz #confusion
table(moje_dane$binary_response,predict.threshold)

Teraz znaleźliśmy optymalny próg myROC$thresholds[idx.which] i możemy go użyć do obcięcia naszych przewidywanych prawdopodobieństw.

Jak już wspomniałem, obszar pod krzywą ROC jest powszechnie stosowany jako kryterium podsumowujące ogólną zdolność predykcyjną naszego modelu. Dobrze jest zdać sobie sprawę, że to właśnie zdolność na wszystkich możliwych progach. Im bliżej 1, tym lepiej. AUC dla losowego klasyfikatora jest równe 0,5, co odpowiada obszarowi pod linią ukośną na powyższym wykresie.

Modele klasyfikacyjne to oczywiście znacznie większa rodzina niż tylko modele regresji logistycznej. Jest to szeroki temat badań. Dobrze jest wiedzieć, że istnieją inne metody, poza "górnym lewym" rogiem do wyboru optymalnych kryteriów, jak np. kryterium Joudena. Kryterium to traktuje czułość i specyfikę jako równie ważne. Jednak nie zawsze tak jest. Trzeba patrzeć na konkretne dane w ręku, bo Twoje ustawienie może być zupełnie inne niż w czyimś tutorialu. Wracając do przykładu z medycyny. Jeśli twoją chorobą jest rak, bardziej martwisz się o fałszywe negatywne obserwacje niż o fałszywe pozytywne. Te fałszywie pozytywne obserwacje będą dalej diagnozowane, ale pominięcie niektórych pacjentów z rakiem może spowodować ich śmierć. W tym ustawieniu będziesz raczej maksymalizować czułość za cenę specyficzności. Z drugiej strony, jeśli twoją chorobą jest HIV, prawdopodobnie jesteś równie zaniepokojony obiema, fałszywie negatywnymi i fałszywie pozytywnymi pacjentami.

Powodzenia w pracy z modelami!