Gemengde ANOVA in R

Stel dat we gegevens hebben van de vorm:

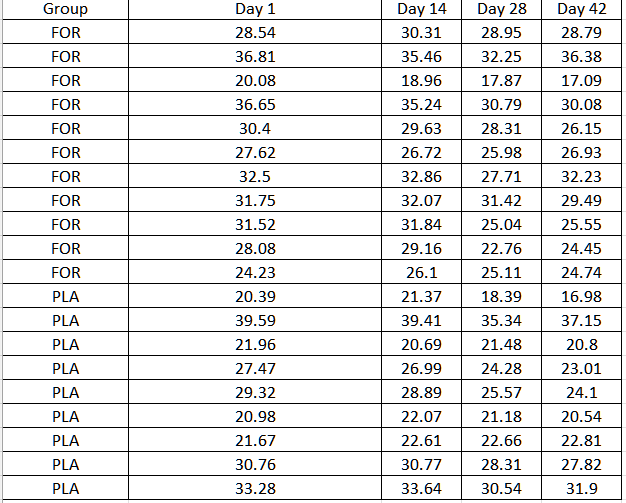
En we willen graag weten of er een interactie-effect was tussen groep, tijd of groep*tijd.

Eerst lezen we de gegevens en zetten ze om in een lang formaat:

bibliotheek(openxlsx)

bibliotheek(lme4)
bibliotheek(afex) #voor p-waarden

bibliotheek(ggplot2)
bibliotheek(gtsummary)#voor mooie tabellen

#lees de gegevens (zet hier het pad naar je bestand)
data.rep<-read.xlsx ("C:/Users/mmura/OneDrive/Dokumenty/FB/data.xlsx")

hoofd(gegevens.rep)
dim(gegevens.rep)

1TP4Maak een data in een lang formaat, en voeg een ID toe voor individuen

data.long<-as.data.frame(cbind(ID=rep(seq(1:20),4),time=rep(c(1,14,28,42),each=20),
          resp=c(data.rep$Day.1,data.rep$Day.14,data.rep$Day.28,data.rep$Day.42),
          group=rep(data.rep$Group,4))
hoofd(data.long)

data.long$time<-as.numeric(data.long$time)
data.long$resp<-as.numeric(data.long$resp)

Tegelijkertijd voegen we een ID-variabele toe voor individuen. Dit kunnen platen/metingen zijn of wat er ook werd gemeten onder de veranderende omstandigheden.

Als volgende stap doen we wat visualisatie:

#Maak een visualisatie

#individuele profielen
ggplot(data.long, aes(x=tijd, y=resp,color=ID)) + geom_smooth()+geom_point()+
  ylab("Uw respons")+xlab("Tijd (dagen)")

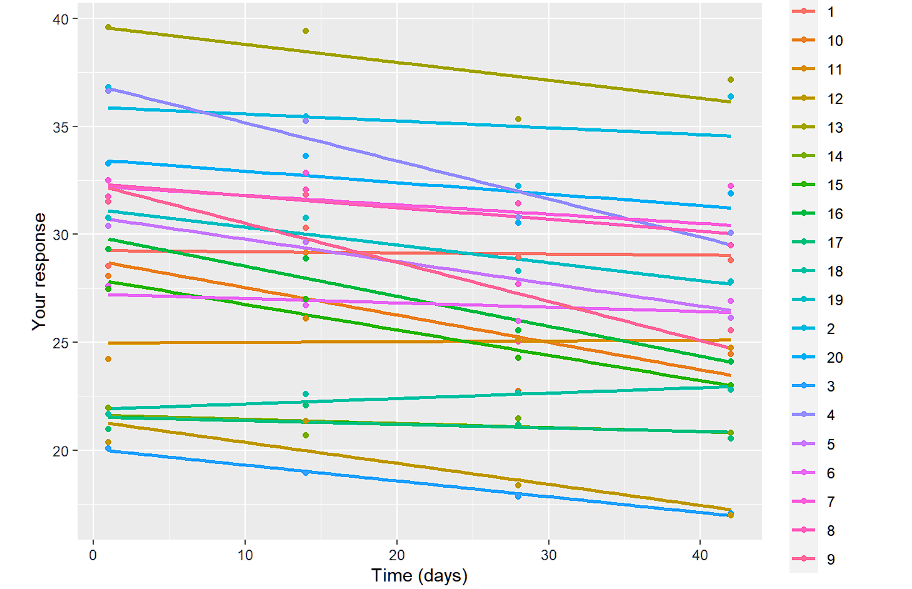
1TP4Nu de lineaire op ID
ggplot(data.long, aes(x=tijd, y=resp,color=ID)) + geom_smooth(methode = "lm",se=FALSE)+geom_point()+
  ylab("Uw reactie")+xlab("Tijd (dagen)")

#daaruit concluderen we dat we ook willekeurige hellingen kunnen opnemen

#gerangschikt per groep
ggplot(data.long, aes(x=tijd, y=resp,kleur=groep)) + geom_smooth()+geom_point()+
  ylab("Uw reactie")+xlab("Tijd (dagen)")

1TP4Nu de lineaire per groep
ggplot(data.long, aes(x=tijd, y=resp,kleur=groep)) + geom_smooth(methode = "lm",se=FALSE)+geom_point()+
  ylab("Uw reactie")+xlab("Tijd")

We tonen hieronder alleen de lineaire plots:

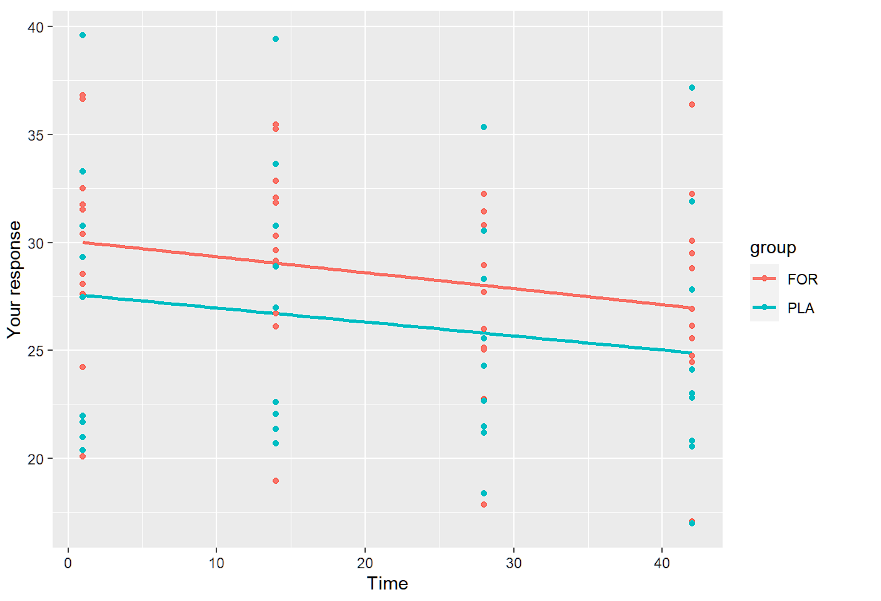
Het doel van deze visualisaties is om te zien of we random intercept en slope nodig hebben en of het lineaire model überhaupt het juiste lijkt te zijn. Door de profielen per groep te inspecteren zien we ook wat we kunnen verwachten. De profielen lopen parallel, dus het groep*tijd effect zal niet significant zijn.

Daarna passen we het initiële model aan:

#Passen van een model
m.initial<-lmer(resp~tijd*groep+(1+tijd|ID),data=data.long)
samenvatting(m.initiaal)
tbl_regressie(m.definitief)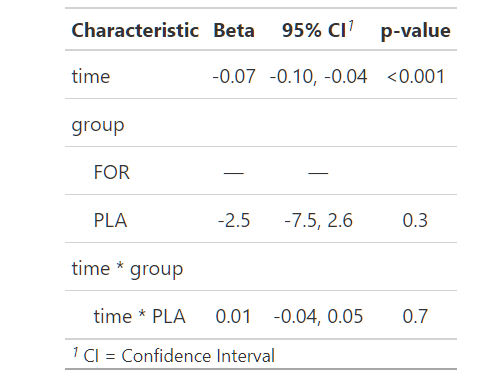

Omdat het interactie-effect niet significant is, verwijderen we het uit het model:

#SOmdat groep*tijd niet significant is, sluiten we deze uit.

m.2<-lmer(resp~tijd+groep+(1+tijd|ID),data=data.long)
samenvatting(m.2)

Het hoofdeffect van de groep is ook niet significant. Daarom zal in het uiteindelijke model alleen het vaste tijdseffect worden gebruikt:

m.final<-lmer(resp~time+(1+time|ID),data=data.long)
samenvatting(m.definitief)


tbl_regressie(m.definitief)

Daarom luidt de eindconclusie als volgt:

Het negatieve trendeffect is significant in het uiteindelijke gemengde model. Gemiddeld daalt de respons met elke dag met 0,07 eenheden.

Het uiteindelijke RMD-bestand is hier.

En de gegevens zijn hier.