ROC-Kurve - was Sie schon immer wissen wollten, aber nicht zu fragen wagten...

Dieser Beitrag wurde, wie viele andere auch, durch die Frage des Studenten inspiriert. Es scheint, dass viele von uns ROC-Kurven in der Analyse verwenden, ohne wirklich zu wissen, wofür diese Kurven sind und wie sie erstellt werden.

Die Klassifizierungsmodelle sind zu einem sehr beliebten Werkzeug geworden und sind Teil vieler implementierter, weithin verfügbarer Black-Box-Lösungen, oft als Teil von Tools für maschinelles Lernen. Einerseits ist diese einfache Verfügbarkeit von gebrauchsfertigen Tools sehr verlockend und ermutigt die Menschen, sie auszuprobieren. Andererseits sucht niemand nach zusätzlichem Wissen über die Methode, da sie vorgegeben ist. Sehr oft sieht man den implementierten Code solcher Klassifikationsmodelle nicht. Daher ist nicht klar, was sich hinter dieser Blackbox verbirgt.

Nehmen wir ein Beispiel aus der Medizin. Nehmen wir an, wir haben eine binäre 0-1-Antwort, die angibt, ob ein Patient krank (1) oder gesund (0) ist. Darüber hinaus haben wir einige Daten über die Patienten, von denen wir glauben oder wissen, dass sie potenzielle Prädiktoren für die Wahrscheinlichkeit, krank oder gesund zu sein, sein könnten, wie z. B. Alter, BMI, Geschlecht oder Rauchen. Das Modell, das unseren binären Prädiktor mit der linearen Kombination der Prädiktoren verknüpft, wird logistisches Regressionsmodell genannt. Es ist die Verallgemeinerung des bekannten linearen normalen Regressionsmodells, aber dieses Mal ist unsere Antwort binär, nicht kontinuierlich, und wir müssen diese binäre Antwort mit dem linearen Teil des Modells verbinden. Dies geschieht über die sogenannte Link-Funktion, die eine Logit-Funktion für das logistische Regressionsmodell ist. In R sieht der Code zur Anpassung eines logistischen Regressionsmodells folgendermaßen aus:

my_model<-glm(binary_response~ age + smoke + bmi + gender,family=binomial, data=my_data))
summary(mein_Modell)

Das obige Modell könnte ein endgültiges Modell sein, nachdem ein stückweises Aufbauverfahren angewandt wurde, um den endgültigen Satz signifikanter Prädiktoren zu erhalten. Oder wir möchten diese Prädiktoren an unseren Daten testen, da wir aus der Literatur wissen, dass sie sich in anderen Studien als signifikant erwiesen haben.

Beachten Sie, dass wir aus zwei Gründen Modelle erstellen:

1. Für die Inferenz, um die Schlussfolgerungen zu ziehen. Dann sollten wir die nicht signifikanten Prädiktoren eliminieren, z. B. mit einem Rückwärts-Eliminierungsverfahren.
2. Für Vorhersagezwecke. Dann kann das Modell übererfüllt sein. Es ist uns nicht so wichtig, was drin ist, solange es eine gute Vorhersagefähigkeit hat.

Konzentrieren wir uns auf diesen zweiten Zweck, denn hier kommt die ROC-Kurve ins Spiel. Aber das Wichtigste zuerst. Nachdem wir das Modell angepasst haben, wollen wir sehen, wie gut die Vorhersage dieses Modells ist. Idealerweise sollten wir unser Modell auf den so genannten Trainingsset und testen Sie es dann an der anderen Testreihe. Es können dieselben Daten sein, aber wir verwenden nur einen Teil davon als Trainingsteil und einen anderen Teil als Testteil. Die Frage, die sich stellt, ist, in welchem Verhältnis wir das tun sollten. Das ist nicht trivial und ist ein Thema der sogenannten Kreuzvalidierung Methoden. Idealerweise sollten wir verschiedene Splits untersuchen und dieses Verfahren durch zufällige Stichproben aus unseren Daten wiederholen. Nehmen wir einmal an, dass wir unsere Pilotdaten hatten, die zur Erstellung eines Modells verwendet wurden, und dass wir nun neue Daten haben, für die wir die Leistung unseres Modells überprüfen wollen.

Zunächst erstellen wir anhand des angepassten logistischen Modells Vorhersagen für unsere Antwort.

vorhergesagt<-vorhersagen(mein_Modell,type=c("Antwort"))

Es ist wichtig zu wissen, dass es sich um eine Wahrscheinlichkeit handelt, die vorhergesagt wird, und nicht um eine binäre Antwort. Nehmen wir an, die Vorhersage für Patient X sei 0,7. Bedeutet das, dass er/sie krank ist? Nun, wenn wir davon ausgehen, dass jeder mit einer Wahrscheinlichkeit >0,5 krank ist, dann ja, er/sie ist nach unserem Modell krank. Die Wahl von Schwellenwert 0,5 ist hier entscheidend. Nachdem wir zum Beispiel 0,5 gewählt haben, können wir die Leistung des Modells untersuchen.

vorhergesagter Schwellenwert  mein_Schwellenwert)

Wenn wir für my_treshold den Wert 0,5 wählen, wird die Antwort von precited.treshold binär sein. Sie ist 1 für die Wahrscheinlichkeiten >0,5 und sonst 0. Dann können wir uns die Konfusionsmatrix ansehen.

table(meine_daten$binary_response,predicted.threshold)

vorhergesagte.Schwelle
    
      0 1
  0 25 304
  1 13 258

Aus dieser Konfusionsmatrix können wir ersehen, wie viele falsch positiv (FP) Die Beobachtungen, die wir haben, sind diejenigen, die vom Modell als krank (1) vorhergesagt wurden, aber gesund sind. Darüber hinaus haben wir falsch negativ (FN) Beobachtungen, d. h. diejenigen, die als gesund vorhergesagt wurden, aber tatsächlich krank sind. Der Rest der Beobachtungen wird echte positive Ergebnisse (TP)richtig vorausgesagt, als krank und echte Negative (TN)richtig als gesund vorausgesagt.

Das gemeinsame Maß zur Bewertung der Modellleistung ist Empfindlichkeit=TP/P, d. h. der Anteil aller als krank erkannten Patienten (P). Ein zweites Maß ist die sogenannte Spezifität=TN/Ndas ist der Anteil aller gesunden Patienten, die als gesund erkannt werden.

Niemand sagt uns, dass unser Schwellenwert 0,5 sein muss. Warum nicht 0,6? Wenn wir den Schwellenwert ändern, ändern sich die Vorhersagen, die Konfusionsmatrix und die Sensitivität und Spezifität ändern sich.

Wie wählt man diesen Schwellenwert, um die Spezifität und Sensitivität zu maximieren? Die Idee ist, beides hoch zu halten. Aber sobald die Empfindlichkeit steigt, sinkt die Spezifität und umgekehrt. Es ist ein Kompromiss zwischen diesen beiden Faktoren.

Müssen wir den Code also für all diese möglichen Schwellenwerte ausführen? Nein, die ROC-Kurve wird das für uns tun.

bibliothek(pROC)

myROC<- roc(my_data$binary_response ~ predicted)

plot(myROC)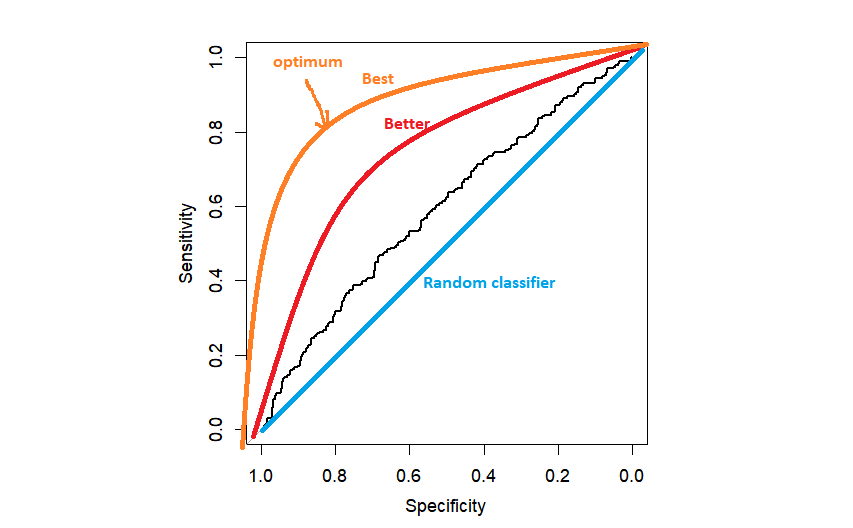

In der Praxis erhalten wir vielleicht so etwas wie die schwarze ROC-Kurve, nur ein bisschen besser als ein zufälliger Klassifikator. Je näher die ROC-Kurve an der linken oberen Ecke liegt, desto besser, weil wir näher an der maximalen Spezifität=1 und der maximalen Sensitivität=1 sind.

Die nächste Frage lautet wie die Schwelle zu wählen ist. Die beliebteste Methode ist die Wahl des Schwellenwerts, der den Abstand zur linken oberen Ecke maximiert. Dies kann automatisch von R durchgeführt werden, aber es ist gut, es einmal selbst zu programmieren.

topleft<-(1-meinROC$-Empfindlichkeiten)^2+(1-meinROC$-Spezifitäten)^2
topleft.threshold<-welcher(topleft==min(topleft))
text(x=meineROC$-Spezifitäten[obererBereich.Schwellenwert], y=meineROC$-Empfindlichkeiten[obererBereich.Schwellenwert],"(0.50,0.58)",col=2)

Sobald wir den optimalen Punkt gefunden haben, können wir ihn mithilfe der Textfunktion in das Diagramm eintragen. An diesem Punkt hört man normalerweise auf und gibt schließlich AUC (Fläche unter der Kurve) als die gesamte Vorhersagefähigkeit des Modells an. Aber wir sollten hier nicht aufhören. Wir wollen herausfinden, welcher Schwellenwert (der Cutoff-Punkt) dem optimalen Punkt für Sensitivität und Spezifität entspricht.

# für eine bestimmte Empfindlichkeit und Spezifität
idx.which<-which((meineROC$-Spezifitäten==0,50)&(meineROC$-Empfindlichkeiten==0,58))

1TP4Nun nehmen wir den Schwellenwert
myROC$hresholds[idx.which]

predict.treshold  myROC$thresholds[idx.which])
#-Verwechslungsmatrix
table(my_data$binary_response,predict.threshold)

Jetzt haben wir den optimalen Schwellenwert myROC$thresholds[idx.which] gefunden und können ihn verwenden, um unsere vorhergesagten Wahrscheinlichkeiten zu reduzieren.

Wie ich bereits erwähnt habe, wird die Fläche unter der ROC-Kurve üblicherweise als Kriterium verwendet, um die Gesamtvorhersagefähigkeit unseres Modells zusammenzufassen. Es ist gut zu wissen, dass es die Fähigkeit ist für alle möglichen Schwellenwerte. Je näher an 1, desto besser. Der AUC für den Zufallsklassifikator ist gleich 0,5, was der Fläche unter der diagonalen Linie in der obigen Grafik entspricht.

Die Klassifikationsmodelle sind natürlich eine viel größere Familie als nur die logistischen Regressionsmodelle. Das ist ein weites Feld der Forschung. Es ist gut zu wissen, dass es neben der "linken oberen Ecke" noch andere Methoden gibt, um das optimale Kriterium zu wählen, z. B. das von Jouden. Bei diesem Kriterium werden Sensitivität und Spezifität als gleich wichtig betrachtet. Dies ist jedoch nicht immer der Fall. Man muss sich die vorliegenden Daten genau ansehen, denn Ihre Einstellung kann völlig anders sein als die in einem anderen Lernprogramm. Um auf das medizinische Beispiel zurückzukommen. Wenn es sich bei Ihrer Krankheit um Krebs handelt, machen Sie sich mehr Sorgen über die falsch negativen Beobachtungen als über die falsch positiven. Diese Falsch-Positiven werden zwar weiter diagnostiziert, aber wenn man einige Krebspatienten übersieht, könnte das deren Tod bedeuten. In diesem Fall werden Sie eher die Sensitivität auf Kosten der Spezifität maximieren. Handelt es sich bei Ihrer Krankheit hingegen um HIV, sind Sie wahrscheinlich gleichermaßen besorgt über falsch negative und falsch positive Patienten.

Viel Glück mit Ihren Modellen!