نمذجة التأثيرات الزمنية في تحليل بيانات المجموعة

لنفترض أن لدينا بيانات على الصورة:

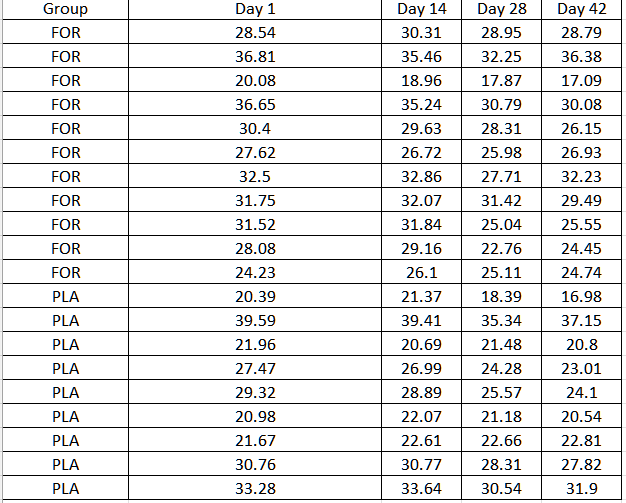
ونود أن نعرف ما إذا كان هناك أي تأثير تفاعلي بين المجموعة أو الوقت أو المجموعة*الوقت.

نقوم أولاً بقراءة البيانات وتحويلها إلى تنسيق طويل:

مكتبة (openxlsx)

مكتبة(lme4)
مكتبة(afex) # للقيم p-قيم

مكتبة(ggplot2)
مكتبة(gtsummary)#للجداول اللطيفة

# للبيانات (ضع المسار إلى ملفك هنا)
data.rep<-read.xlsx ("C:/Users/mmura/OneDrive/Dokumenty/FB/data.xlsx")

رأس(data.rep)
خافت(data.rep)

1TP5صنع بيانات بتنسيق طويل، مع إضافة بعض المعرفات للأفراد

data.long<-as.data.frame(cbind(cbind(ID=rep(seq(1:20),4),time=rep(c(1,14,28,42),each=20),
          resp=ج(data.rep$Day.1,data.rep$Day.14,data.rep$Day.28,data.rep$Day.42),
          group=rep(data.rep1.rep$Group,4)))
رأس(data.long)

data.long$ime<-as.numeric(data.long$ime)
data.long$resp<-as.as.numeric(data.long$resp)

في الوقت نفسه، نضيف بعض المتغيرات التعريفية للأفراد. يمكن أن يكون ذلك لوحات/مقاييس أو أي شيء تم قياسه في ظل الظروف المتغيرة.

كخطوة تالية، نقوم ببعض التصورات:

1TP5صنع بعض التصور

1TP5ملامح فردية
ggplot(data.long, aes(x=وقت, y=resp,color=ID)) + geom_smooth()+ geom_smooth()+geom_point()+
  ylab("استجابتك")+xlab("الوقت (بالأيام)")

1TP5الآن الخطي حسب المعرف
ggplot(data.long, aes(x=وقت, y=resp,color=ID)) + geom_smooth(method = "lm"، se=FALSE)+geom_point()+
  ylab("استجابتك")+xlab("الوقت (أيام)")

#من ذلك نستنتج تضمين المنحدرات العشوائية أيضًا

#smoothed حسب المجموعة
ggplot(data.long, aes(x=وقت, y=resp,color=group)) + geom_smooth()+ geom_smooth()+geom_point()+
  ylab("استجابتك")+xlab("الوقت (أيام)")

1TP5الآن الخطي حسب المجموعة
ggplot(data.long, aes(x=وقت, y=resp,color=group)) + geom_smooth(method = "lm",se=FALSE)+geom_point()+
  ylab("استجابتك")+xlab("الوقت")

نعرض فقط المخططات الخطية أدناه:

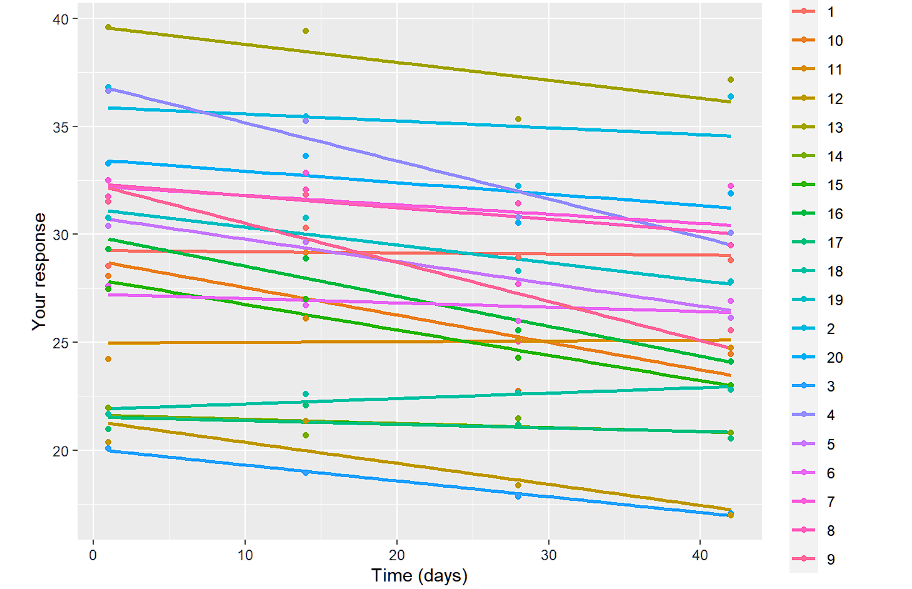
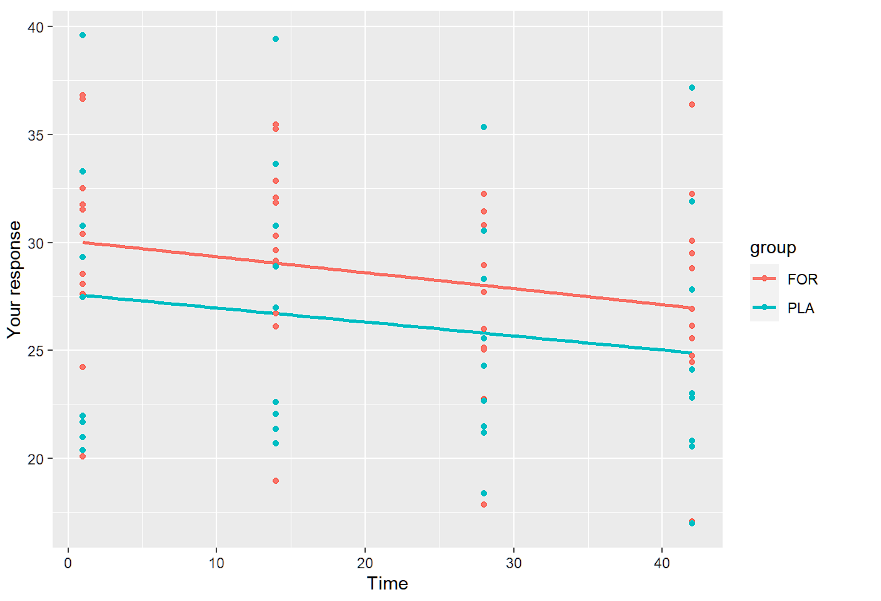
والغرض من هذه التصورات هو معرفة ما إذا كنا بحاجة إلى اعتراض وميل عشوائي وما إذا كان النموذج الخطي يبدو صحيحًا في المقام الأول. أيضًا، من خلال فحص الملامح حسب المجموعة نرى ما يمكن توقعه. الملامح متوازية، لذا فإن تأثير المجموعة*الزمن لن يكون كبيراً.

ثم نطابق النموذج الأولي:

1TP5تركيب نموذج
m.initial<-lmer(resp~ time*group+(1+ time|ID),data=data.long)
ملخص(m.initial)
tbl_regression(m.final)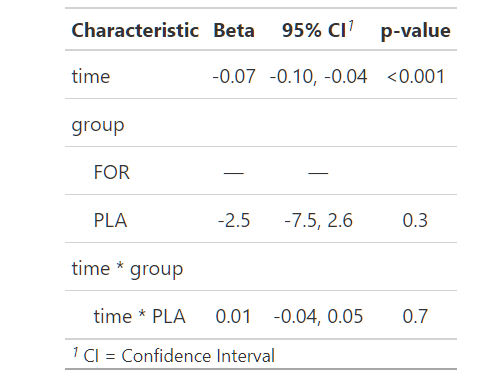

ونظرًا لأن التأثير التفاعلي غير مهم، فإننا نحذفه من النموذج:

#S بما أن المجموعة*الوقت غير مهم فإننا نستبعده

م.2<-مر(resp~الوقت+المجموعة+(1+الوقت|المعرف),البيانات=data.long)
ملخص(m.2)

كما أن تأثير المجموعة الرئيسية ليس ذا دلالة. لذلك، لن يكون هناك في النموذج النهائي سوى التأثير الزمني الثابت:

m.final<-lmer(resp~ time+(1+ time|ID),data=data.long)
ملخص(m.final)


tbl_regression(m.final)

لذلك، فإن الاستنتاج النهائي هو التالي:

تأثير الاتجاه السلبي كبير في النموذج المختلط النهائي. في المتوسط مع كل يوم واحد، تنخفض الاستجابة بمقدار 0.07 وحدة.

ملف RMD النهائي هو هنا.

والبيانات هي هنا.

ANOVA المختلط في R

اترك تعليقاً إلغاء الرد