关于单个比例的样本量计算的几点思考

假设我们需要为单个比例估计（测试）计算样本量。现在省略数学和使用的公式中的某些可变性，我们可以通过两种方式做到这两种：

首先：使用单个测试的功效，然后我们仅要求测试是否拒绝给定比例为零的假设（通常基于双面测试）。

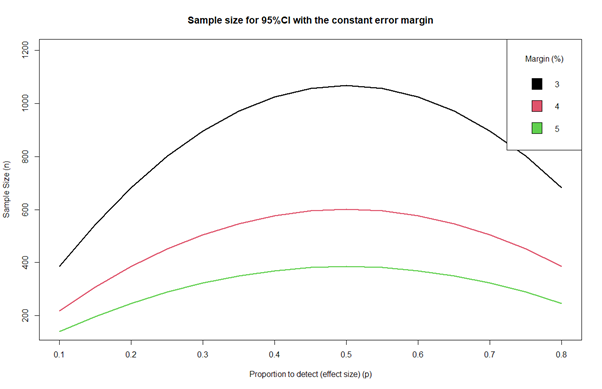
第二：使用95%CI和所需的误差容限（误差容限= 95%CI的一半）。固定边距的问题在于，当我们估计50%或70%比例时，5%余量是不同的，而当我们估计20%比例时，则不同。

第一种方法结果：

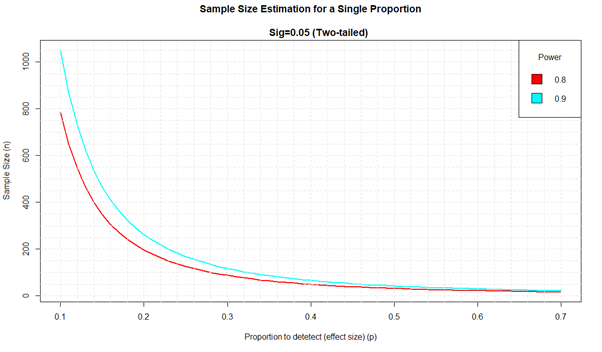
这是我们针对第一种方法针对不同的功率和效果大小值进行仿真的结果。

因此，例如要估计比例为0.2，我们需要两侧95%CI的n = 263，功率为0.9。

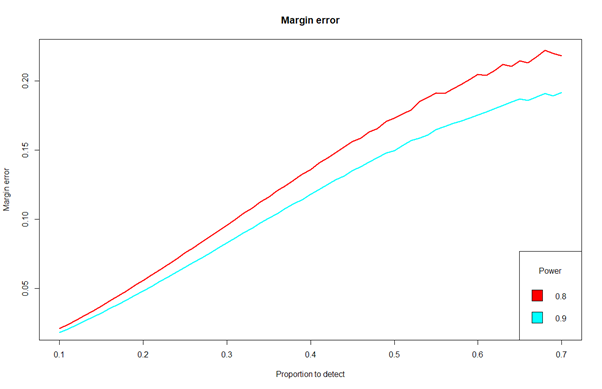
请注意，对于该方法，95%CI的误差容限不是固定的（有些人显然不知道）。它以估计的比例增长（请参阅下面的第二个图），这是合乎逻辑的，因为我们不需要70%比例估计（通常）需要5%余量。对于70%，我们在20%周围有一个余量，这与20%比例所占的5%余量相比要少得多。

因此，对于以20%比例进行估算的示例，第一种方法将给我们带来的准确误差为4.83%。换句话说，使用95%CI估计最小预期比例为0.2，误差范围为4.83%，我们需要263名患者。

第二种方法基于修正边距误差（第三幅图）。如您所见，在这种情况下，样本大小的函数始终在p = 0.50处具有最大值。因此，如果要固定边距，则可以选择最大n作为最坏情况。

这两种方法之间的差异来自于以下事实：在第一种方法中，95%CI的估计与否定原假设所需的宽度一样窄。通过在第二种方法中要求较小的保证金，您将付出更大的样本量和更好的估计准确性的代价。

选择哪种方法？这取决于您的目标。如果您需要较小的样本拾取方法1，但要注意误差范围。如果您需要更好的评估方法，并且可以召集更多的人，则方法2是可行的。