Einige Gedanken zur Berechnung der Stichprobengröße für einen einzelnen Anteil

Angenommen, wir müssen eine Stichprobengröße für eine einzelne Proportionsschätzung (Test) berechnen. Wenn wir jetzt Mathematik und eine gewisse Variabilität in den verwendeten Formeln weglassen, können wir dies auf zwei Arten tun:

Erstens: Wenn Sie die Leistung eines einzelnen Tests verwenden und dann nur noch verlangen, dass der Test die Hypothese eines bestimmten Anteils als Null ablehnt oder nicht (normalerweise basierend auf einem zweiseitigen Test).

Zweitens: Verwenden der 95%CI und der gewünschten Fehlergrenze (Fehlergrenze = die Hälfte der 95%CI). Das Problem bei der Festlegung der Marge besteht darin, dass die 5%-Marge etwas anderes ist, wenn wir den 50%- oder 70%-Anteil schätzen, und anders, wenn wir den 20%-Anteil schätzen.

Ergebnisse des ersten Ansatzes:

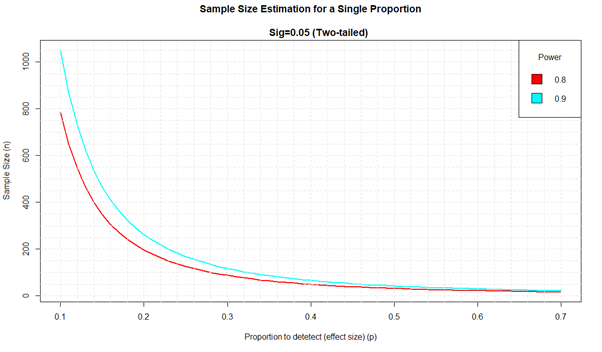
Dies haben wir als Ergebnis der Simulation für verschiedene Werte von Leistung und Effektgröße für den ersten Ansatz erhalten.

Um beispielsweise einen Anteil von 0,2 zu schätzen, benötigen wir n = 263 für zweiseitige 95%CI und Leistung 0,9.

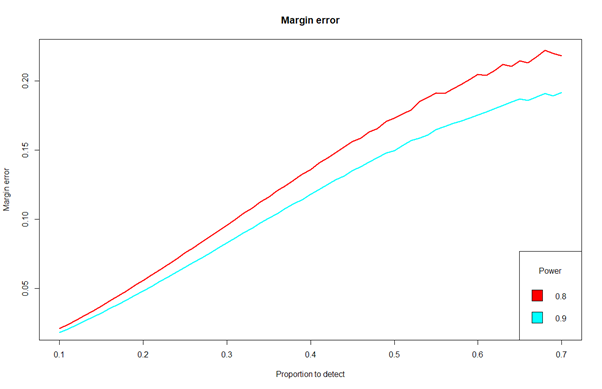
Beachten Sie, dass für diese Methode die Fehlergrenze für 95%CI nicht festgelegt ist (was einigen Personen offensichtlich nicht bekannt ist). Es wächst mit dem geschätzten Anteil (siehe das zweite Diagramm unten), was logisch ist, da wir für die Schätzung des 70%-Anteils (normalerweise) keine 5%-Marge benötigen. Für 70% haben wir eine Marge um 20%, die mit einer Marge von 5% für 20% vergleichbar ist.

In unserem Beispiel mit einem Anteil von 20% zur Schätzung der ersten Methode erhalten wir also einen Margenfehler von genau 4,83%. Mit anderen Worten, um den erwarteten Mindestanteil von 0,2 mit der Fehlerquote 4,83% unter Verwendung des 95%CI zu schätzen, benötigen wir 263 Patienten.

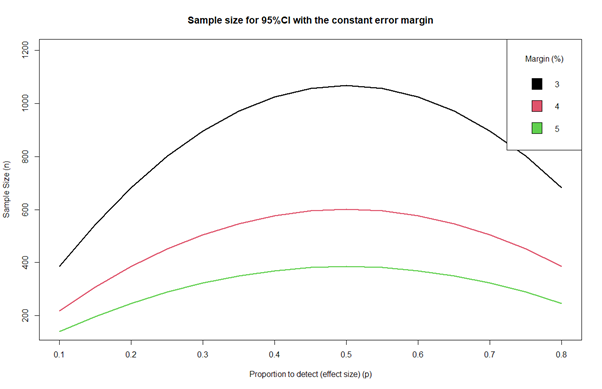
Der zweite Ansatz basiert auf der Behebung eines Randfehlers (drittes Diagramm). Wie Sie sehen können, hat die Funktion der Stichprobengröße in diesem Fall immer ein Maximum bei p = 0,50. Wenn Sie also eine Marge festlegen möchten, können Sie das Maximum n als Worst-Case-Szenario auswählen.

Die Diskrepanz zwischen diesen beiden Methoden beruht auf der Tatsache, dass 95%CI im ersten Ansatz genauso eng geschätzt wird, wie es zur Ablehnung der Nullhypothese erforderlich ist. Wenn Sie bei der zweiten Methode nach einer kleineren Marge fragen, zahlen Sie den Preis für die größere Stichprobe, aber eine bessere Schätzgenauigkeit.

Welche Methode soll man wählen? Es hängt von Ihrem Ziel ab. Wenn Sie eine kleinere Probe benötigen, nehmen Sie Methode 1 auf, beachten Sie jedoch die Fehlerquote. Wenn Sie eine bessere Esitmation benötigen und mehr Personen sammeln können, ist die Methode 2 die richtige.