انحدار ديمنج

نعلم جميعًا نماذج الانحدار الخطي OLS الشائعة. في هذا النوع من النماذج، نفترض أن Y تعتمد خطياً على بعض المتنبئات المستمرة X زائداً ونأخذ في الحسبان خطأ القياس ل Y على النحو التالي:

Y_i=A+B*X_i,

i هو مؤشر الملاحظة i على X و Y.

لاحظ أنه من نموذج الانحدار هذا، نظرًا لوجود متنبئ واحد فقط، يمكن تقدير معامل الارتباط الخطي R على النحو التالي

r=R=sqrt(R^2).

لاحظ أيضًا أن اختبار H0:r=0 يعادل اختبار H0:B=0.

يمكن أن يكون X على سبيل المثال الوقت المستغرق في الدراسة للطالب i- و X درجته في الامتحان.

من الناحية المثالية، كلما زاد طول X زاد Y، لذا من المفترض أن يكون معامل B موجبًا.

طريقة ملاءمة هذا النموذج في R هي عبر الدالة:

 lm(Y~X, data=my.data)

ولكن ماذا لو أردنا على سبيل المثال مقارنة جهازين Dev1 و Dev2. نقيس نفس الشيء على Dev1 و Dev2. وكنتيجة لذلك نحصل على متجه المقاييس على Dev1 (X1) و Dev2 (X2). والطريقة لتقييم الاتفاق بين هذين الجهازين هي عن طريق ما يسمى بانحدار ديمينج. هذا الانحدار هو شيء مشابه لانحدار OLS، لكنه يفترض أن كلاً من Y و X مقيسان بالخطأ.

لذلك، بالنسبة للجهاز الأول Dev1 لدينا:

X1_i=A1+B1*TrueX1_i+E2_i

وبالنسبة للجهاز الثاني DEV2:

X2_i=A2+B2*TrueX2_i+E2_i.

في المعادلتين السابقتين E1 وE2 هما الخطأ في القياس.

نفترض أن متجهات الخطأ هذه موزعة بشكل طبيعي مع N(0,sigma1^2) و N(0,sigma2^2). بالإضافة إلى ذلك، نعرّف لامدا=سيجما1^2/سيجما2^2.

اللمبدا هي نسبة التباين لخطأَي القياس. عادةً ما نفترض أن lambda=1 بحيث لا تكون أي من الآلات في صالح أي من الآلتين. طريقة ملاءمة انحدار ديمينج في R هي عبر الحزمة مكرر.

كتبتُ أدناه دالة ترسم نتيجة انحدار ديمينج التي يتم تركيبها عبر دالة mcreg.

كما أنه يعيد أيضًا الميل والجزء المقطوع الذي تم الحصول عليه من النموذج.

Draw.Deming.Deming.Plot<- وظيفة(resp1,resp2,name1){
  #mcreg لا يقبل الصبغيات الصفرية
  df<-as.data.frame(cbind(resp1,resp2))
  df2<- df[حالات كاملة(df)،]
  dem.reg<- mcreg(df2$resp1,df2$resp2, error.ratio = 1, method.reg = "Deming")
  MCResult.plot(dem.reg, equal.axis = TRUE, x.lab = "الجهاز 1", y.lab = "الجهاز 2", points.col = "#FF7F5060", points.pch = 19, ci.area = TRUE, ci.area.col = "#FF7F50", main = paste("Deming Regression for ",name1), sub = "", add.grid = FALSE, points.cex = 1)
  إرجاع(list(list(intercept=c(dem.reg@para[1,c(1,3,4)]),slope=c(dem.reg@para[2,c(1,3,4)])))
}

دعونا نرى الرسم البياني الذي تم إنتاجه لبيانات المثالين resp1 و resp2.

resp1<-c(1,1.2,2,3,4,4.1,5,5.1)
resp2<-c(1,1.3,2.2,3.1,4,4.2,5.1,5.5)
Draw.Deming.Plot(resp1,resp2,"تجربتي")

نحصل على:

$intercept
        EST EST LCI UCI
 0.01532475 -0.18087790 0.19446184

$slope
      EST EST LCI UCI
1.0345434 0.9672911 1.0910989 

والحبكة

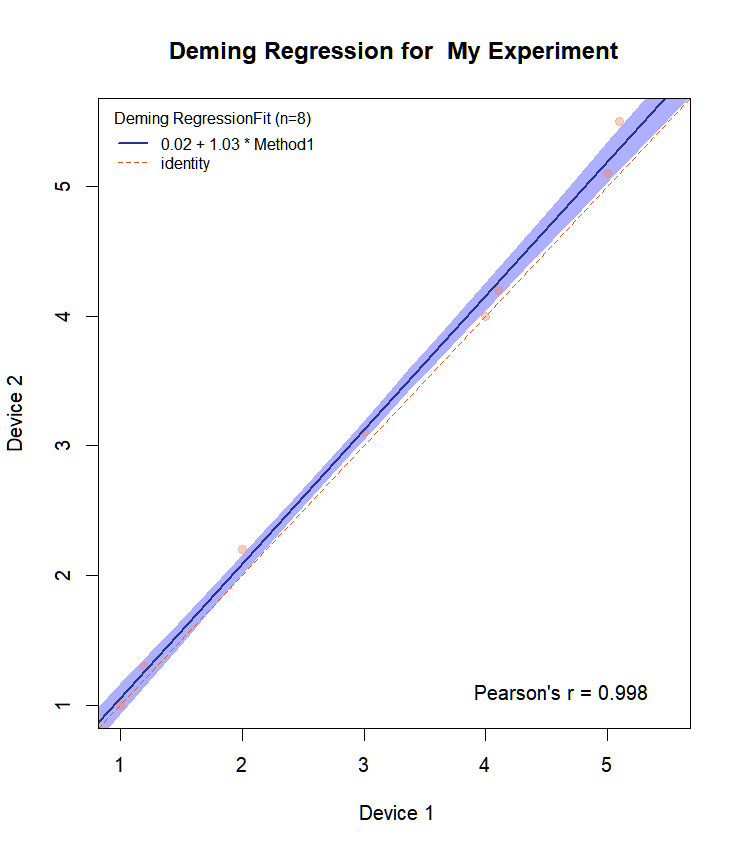
نلاحظ أن الاتفاق المذكور أعلاه يكاد يكون مثاليًا لبيانات هذه اللعبة. الميل يساوي 1 مع حدود الثقة: 0.97-1.09. ترسم الدالة MCResult.plot افتراضيًا أيضًا حدود الثقة باللون المختار. كما أنها تضع المعادلة على الرسم البياني.

إذا أراد المرء أن يضع أيضًا المؤشر الجغرافي للميل والجزء المقطوع على الرسم البياني، فإليك تعديل دالة MCResult.plot():

MCResult.plot2 0 & alpha = الطول (أسماء (أرقام))))
  إذا (is.null(digits$coef)) {
    digits%sP4Tcoef <- 2
  }
  إذا (is.null.null(digits$cor))) { {
    digits$cor <- 3
  }
  طريقة cor.method <- match.arg(cor.method)
  stopifnot(is.element(cor.method, c("pearson", "kendall",
                                     "سبيرمان"))))
  مكان الأسطورة  1)
    إيقاف إذا (طول (point.col) = = nrow(x@data))
  إذا (طول(points.pch)> 1)
    stopifnot(length(length(points.pch) == nrow(x@data))
  إذا (x@regmeth =="LinReg")
    اسم العنوان <- "الانحدار الخطي"
  في حالة أخرى إذا (x@regmeth =="WLinReg")
    اسم العنوان <- "انحدار خطي مرجح"
  غير ذلك إذا (x@regmeth =="TS")
    اسم العنوان <- "الانحدار الخطي المرجح"
  غير ذلك إذا (x@regmeth == "PBequi")
    الاسم العشري <- "انحدار بابلوك المتكافئ الممرر المتساوي"
  غير ذلك إذا (x@regmeth =="Deming")
    اسم العنوان <- "انحدار ديمينج"
  غير ذلك إذا (x@regmeth =="WDeming")
    اسم العنوان <- "انحدار ديمينج المرجح"
  غير ذلك اسم الحلمة <- "انحدار بابلوك الموزون"
  لطيف أزرق <- rgb(37/255, 52/255, 148/255)
  لطيفة <- rgb(230/255، 85/255، 13/255)
  niceblue.bounds <- rgb(236/255, 231/255, 242/255)
  إذا (is.null(reg.col))
    reg.col <- niceblue
  إذا (is.null(identity.col))
    identity.col <- niceor
  إذا (is.null(ci.area.col))
    ci.area.col <- niceblue.bounds
  إذا (is.null(ci.border.col))
    ci.border.col  1)
  إذا (is.null(xlim))
    rx <- النطاق (x@data[, "x"]، na.rm = TRUE)
  غير ذلك rx <- xlim
  tmp.range <- range(as.vector(x@data[, c("x", "y")])، na.rm = TRUE)
  إذا (equ.axis.axis == TRUE) {
    إذا (is.no.null(ylim))) {
      yrange <- tmp.range
    }
    غير ذلك {
      yrange <- ylim
    }
  }
  غير ذلك {
    إذا (is.null(ylim)) { {
      yrange <- المدى(as.vector(x@data[, "y"])، na.rm = TRUE)
    }
    غير ذلك {
      yrange <- ylim
    }
  }
  إذا (!is.null(xlim) & & !is.null(ylim) & equal.axis) { {
    xlim <- c(min(c(xlim[1]، ylim[1]))، max(c(xlim[2]، ylim[2])))
  }
  إذا (is.null(xaxp)) {
    إذا (!is.null(xlim))) {
      axis_ticks <- axisTicks(c(xlim[1] - 0.05 * xlim[2],
                                السقف((xlim[2] + 0.05 * xlim[2]) * 10^digits$coef)/10^digits$coef),
                              لوغاريتم = F، نينت = 7)
      xaxp <- c(axis_ticks[1]، ذيل (axis_ticks, n = 1),
                الطول(axis_ticks) - 1)
      xlim <- ج(axis_ticks[1]، ذيل(axis_ticks، n = 1))
    }
  }
  في حالة أخرى {
    إذا (!is.null(xlim))) { {
      إذا كان ((xlim[1] = = rx[1] && xlim[2] = rx[2])) | (tmp.range[1] ==
                                                    xlim[1] && tmp.range[2] = = xlim[2])) {
        xlim <- c(xaxp[1]، xaxp[2])
      }
    }
    غير ذلك {
      تحذير ("لا يجب تعيين xaxp بدون xlim")
      xaxp <- NULL
    }
  }
  إذا (is.null(yaxp)) {
    إذا (!is.null(ylim) && !equ.axis.equis) {
      yaxp <- ax_ticks <- axis_ticks(c(ylim[1] - 0.05 *
                                          ylim[2]، السقف((ylim[2] + 0.05 * ylim[2])) *
                                                             10^digits$coef)/10^digits$coef)، لوغاريتم = F، nint = 10)
      yaxp = c(c(axis_ticks[1], tail(axis_ticks, n = 1),
               الطول(axis_ticks) - 1)
      ylim <- c(c(axis_ticks[1], tail(axis_ticks, n = 1))
    }
    في حالة أخرى {
      إذا (equal.axis) {
        إذا (!is.null(xlim))) { {
          yaxp <- xaxp
          ylim <- xlim
        }
      }
    }
  }
  آخر { {
    إذا (!is.null(ylim))) { {
      إذا كان ((ylim[1] == yrange[1] && ylim[2] == yrange[2])|
          (tmp.range[1] == ylim[1] && tmp.range[2] == ylim[2])) {
        ylim <- c(yaxp[1]، yaxp[2])
      }
    }
    غير ذلك {
      تحذير("يجب عدم تعيين yaxp بدون ylim")
      yaxp <- NULL
    }
  }
  إذا (equal.axis) {
    إذا (is.null(ylim)) { {
      yaxp <- xaxp
      ylim <- xlim
    }
    إذا (is.null(xlim)) { {
      xaxp <- yaxp
      xlim <- ylim
    }
  }
  إذا (!is.null.null(xlim))) {
    إذا (إذا (xlim[1] < tmp.range[1]) {
      tmp.range.range[1]  tmp.range[2]) { {
      tmp.range.range[2] <- xlim[2]
    }
  }
  إذا (!is.null(ylim)) { {
    إذا (ylim[1] < yrange[1]) {
      yrange[1]  yrange[2]) { {
      yrange[2] <- yrange[2] <- ylim[2]
    }
  }
  xd <- seq(rx[1], rx[2], length.out = xn)
  xd <- اتحاد (xd، rx)
  دلتا <- القيمة المطلقة (rx[1] - rx[2])/xn
  xd <- xd[ترتيب (xd)]
  xd.add <- ج(xd[1] - دلتا * 1:10، xd، xd[طول (xd)] + دلتا *
                1:10)
  إذا (is.null(xlim))
    xlim <- rx
  إذا (ci.area = = TRUE | | ci.border = = TRUE) {
    الحدود <- حدود <- calcResponse(x, alpha = alpha, x.levels = xd)
    bounds.add <- calcResponse(x, alpha = alpha, x.levels = xd.add)
    إذا (equal.axis == TRUE) {
      xd <- seq(tmp.range[1]، tmp.range[2]، length.out = xn)
      xd <- اتحاد (xd، tmp.range)
      دلتا <- القيمة المطلقة (rx[1] - rx[2])/xn
      xd <- xd[ترتيب (xd)]
      xd.add <- c(xd[1] - دلتا * 1:10, xd, xd[طول(xd)] +
                    دلتا * 1:10)
      الحدود <- حساب الاستجابة (x، ألفا = ألفا، مستويات x.levels = xd)
      bounds.add <- calcResponse(x, alpha = alpha, x.levels = xd.add)
      yrange <- المدى(c(as.vector(x@data[, c("x", "y")]),
                        as.vector(bounds[, c("X", "Y", "Y.LCI", "Y.UCI")])),
                      na.rm = TRUE))
    }
    غير ذلك {
      yrange <- النطاق (c(c(as.vector(x@data[, "y"])، as.vector(bounds[,
                                                                   ج("Y", "Y.LCI", "Y.UCI")])، na.rm = TRUE)
    }
  }
  في حالة أخرى {
    إذا (equal.axis == TRUE) { {
      yrange <- tmp.range
    }
    غير ذلك { {
      yrange <- المدى (as.vector(x@data[, "y"])، na.rm = TRUE)
    }
  }
  إذا (equal.axis) {
    إذا (is.null(ylim)) { {
      xlim <- ylim <- tmp.range
    }
    غير ذلك {
      xlim <- ylim
    }
  }
  غير ذلك {
    إذا (is.null(xlim))
      xlim <- rx
    إذا (is.null(ylim))
      ylim <- yrange
  }
  إذا (is.null(main)))
    رئيسي <- لصق (اسم الحلم، "مناسب")
  إذا (!إضافة) {
    رسم (0، 0، 0، cex = 0، ylim = ylim، xlim = xlim، xlab = x.lab,
         ylab = y.lab، رئيسي = رئيسي، فرعي = ""، xaxp = xaxp,
         yaxp = yaxp، bty = "n"، ...)
  }
  آخر {
    فرعي <- ""
    add.legend <- FALSE
    إضافة شبكة <- FALSE
  }
  إذا (add.legend.add.legend == TRUE) {
    إذا كانت (الهوية == TRUE & reg == TRUE) {
      نص2 <- "هوية"
      text1 <- النص1 <- لصق (formatC(round(x@para["Intercept",
                                          "EST"]، الأرقام = digits$coef)، الأرقام = digits$coef,
                             format = "f"),"("(",formatC(round(x@para["Intercept",
                                                                    "LCI"]، أرقام = digits$coef)، أرقام = digits$coef,
                                                       format = "f"),";"؛",formatC(round(x@para["Intercept",
                                                                                          "UCI"]، أرقام = digits$coef)، أرقام = digits$coef,
                                                                             format = "f")،")"،"" + "، formatC(round(x@para["Slope",
                                                                        "EST"]، الأرقام = digits$coef)، الأرقام = digits$coef,
                                                           format = "f"),"(",formatC(round(x@para["Slope",
                                                                                                  "LCI"]، أرقام = digits$coef)، أرقام = digits$coef,
                                                                                     format = "f"),";"؛",formatC(round(x@para["Slope",
                                                                                                                        "UCI"]، أرقام = digits$coef)، أرقام = digits$coef,
                                                                                                           التنسيق = "f")،")")" ," * "،" * "، x@mnames[1]، sep = "")
      وسيلة الإيضاح(legend(legend.place, lwd = c(reg.lwd, identity.lwd),
             lty = c(reg.lty, identity.lty), col = c(reg.col,
                                                     identity.col)، العنوان = paste(titname, "Fit (n=",
                                                                                  dim(x@data)[1], "), ")"، sep = "")، وسيلة الإيضاح = c(text1,
                                                                                                                             text2)، box.lty = "فارغ"، cex = 0.8، bg = "أبيض",
             أقحم = ج(0.01، 0.01)))
    }
    إذا (الهوية = = TRUE & reg = = FALSE) {
      النص2 <- "هوية"
      وسيلة الإيضاح(legend(legend.place, lwd = identity.lwd, lty = identity.lty,
             col = identity.col, title = paste(titname, "Fit (n=",
                                               dim(x@data)[1], "), ")"، sep = "")، وسيلة الإيضاح = text2,
             box.lty = "فارغ"، cex = 0.8، bg = "أبيض"، inset = c(0.01,
                                                                   0.01))
    }
    إذا (الهوية = FALSE & reg = TRUE) {
      text1 <- لصق (formatC(formatC(round(x@para["Intercept",
                                          "EST"]، الأرقام = digits$coef)، الأرقام = digits$coef,
                             format = "f")، "+"، "+"، formatC(round(x@para["Slope",
                                                                      "EST"]، الأرقام = digits$coef)، الأرقام = digits$coef,
                                                         format = "f"), "*", x@mnames[1], sep = "")
      وسيلة الإيضاح(legend(legend.place, lwd = c(2), col = c(reg.col),
             العنوان = لصق(لصق(titname, "Fit (n="، dim(x@data)[1],
                           ")"، sep = "")، وسيلة الإيضاح = c(text1)، box.lty = "فارغ",
             cex = 0.8، bg = "أبيض"، inset = c(0.01، 0.01))
    }
  }
  إذا (ci.area = = TRUE | ci.border = TRUE) {
    إذا (ci.area == TRUE) { {
      xxx <- c(xd.add، xd.add[order(xd.add، تنازلي = TRUE)])
      yy1 <- c(as.vector(bounds.add [، "Y.LCI"]))
      yy2 <- c(as.vector(bounds.add[, "Y.UCI"]))
      yyyy <- c(yy1، yy2[ترتيب(xd.add، تنازلي = TRUE)])
      مضلع(xxx, yyy, col = ci.area.col, border = "أبيض",
              lty = 0)
    }
    إذا (add.grid)
      شبكة()
    إذا (ci.border.border == TRUE) { {
      points(xd.add، bounds.add[, "Y.LCI"]، lty = ci.border.lty,
             lwd = ci.border.lwd، النوع = "l"، col = ci.border.col)
      نقاط(xd.add، bounds.add [، "Y.UCI"]، lty = ci.border.lty,
             lwd = ci.border.lwd, type = "l", col = ci.border.col)
    }
    إذا (is.null(sub))) {
      إذا (x@cimeth %in% c("bootstrap", "nestedbootstrap"))
        نص فرعي <- لصق ("The "، 1 - x@alpha, "-تم حساب حدود الثقة باستخدام ",
                         x@cimeth, "(", x@bootcimeth, ").", sep = "")
      وإلا إذا ((x@regmeth = == "PaBa") & (x@cimeth == "تحليلي"))
        نص فرعي <- ""
      نص فرعي آخر <- النص الفرعي <- لصق ("The"، 1 - x@alpha, "-يتم حساب حدود الثقة باستخدام طريقة ",
                            x@cimeth, " طريقة.", sep = "")
    }
    نص فرعي آخر <- فرعي
  }
  غير ذلك {
    إذا (add.grid)
      الشبكة()
    النص الفرعي <- إن كان النص الفرعي (is.null(sub)، ""، الفرعية)
  }
  إذا (add.cor == TRUE) { {
    cor.coef <- لصق (formatC(formatC(round(cor(cor(x@data[, "x"], x@data[,
                                                              "y"]، الاستخدام = "pairwise.complete.obs"، الطريقة = cor.method),
                                    digits = digits$cor)، digits = digits$cor، التنسيق = "f"))
    إذا (cor.method = = "pearson")
      cortext <- لصق ("r بيرسون = "، cor.coef، sep = "")
    إذا (cor.method == "kendall")
      cortext <- b- bquote(paste("Kendall's ", tau, " = ",
                              .(cor.coef)، sep = "")))
    إذا (cor.method == "spearman")
      cortext <- b- bquote(لصق ("سبيرمان", rho, " = ",
                              .(cor.coef)، sep = "")))
    mtext(الجانب = 1، الخط = -2، cortext، adj = 0.9، الخط = 1)
  }
  إذا (draw.points = = TRUE) { {
    نقاط(x@data[, 2:3]، col = points.col, pch = points.pch,
           cex = points.cex، ...)
  }
  العنوان(sub(sub = subtext)
  إذا (reg = = TRUE) {
    b0 <- b0 <- x@para["اعتراض"، "EST"]
    ب1 <- b1 <- x@para["الميل"، "EST"]
    خط (b0، b1، lty = reg.lty، lwd = reg.lwd، col = reg.col)
  }
  إذا (الهوية = = TRUE) {
    abline(0, 1, lty = identity.lty, lwd = identity.lwd,
           العمود = identity.col)
  }
  مربع()
}

إذا قمنا بتغيير الدالة الآن

Draw.Deming.Deming.Plot<- وظيفة(resp1,resp2,name1){
  #mcreg لا يقبل الصبغيات الصفرية
  df<-as.data.frame(cbind(resp1,resp2))
  df2<- df[حالات كاملة(df)،]
  dem.reg<- mcreg(df2$resp1,df2$resp2, error.ratio = 1, method.reg = "Deming")
  MCResult.plot2(dem.reg, equal.axis = TRUE, x.lab = "الجهاز 1", y.lab = "الجهاز 2", points.col = "#FF7F5060", points.pch = 19, ci.area.area.= TRUE, ci.area.col = "#FF7F50", main = paste("Deming Regression for ",name1), sub = "", add.grid = FALSE, points.cex = 1)
  إرجاع(list(list(intercept=c(dem.reg@para[1,c(1,3,4)]),slope=c(dem.reg@para[2,c(1,3,4)])))
}

ونحن نتصل

Draw.Deming.Plot(resp1,resp2,"تجربتي")

ثم نحصل على:

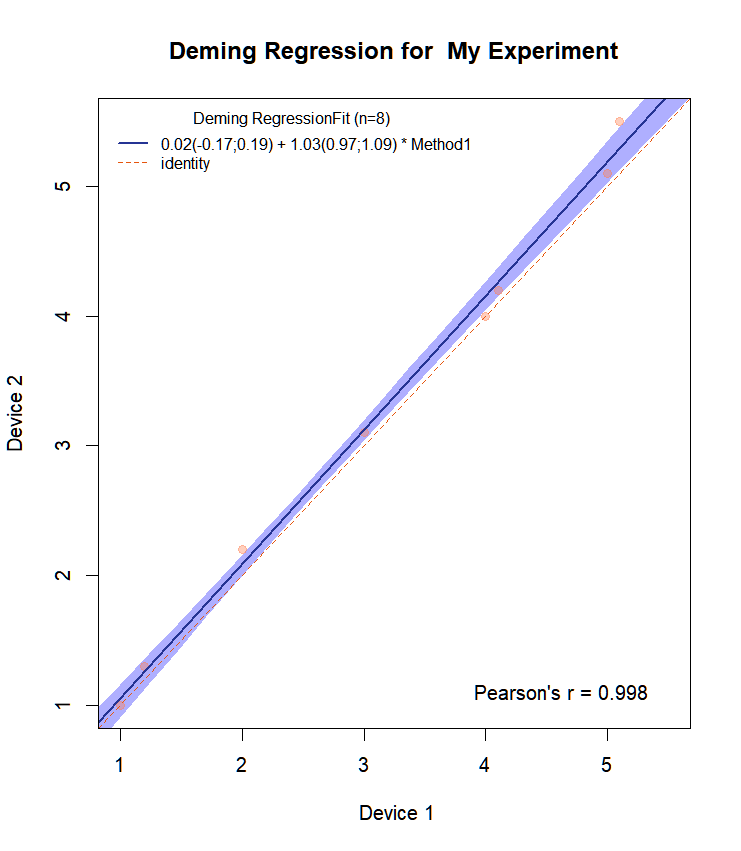
يحتوي الآن على كل CI للميل والجزء المقطوع على الرسم البياني.

استمتع بوقتك!