قلة الأفكار حول حساب حجم العينة لنسبة واحدة

لنفترض أننا بحاجة إلى حساب حجم عينة لتقدير نسبة واحدة (اختبار). بحذف الرياضيات الآن وبعض التباين في الصيغ المستخدمة ، يمكننا القيام بذلك بطريقتين:

أولاً: استخدام قوة اختبار واحد ثم نطلب فقط أن يكون الاختبار هو رفض أو عدم فرضية نسبة معينة لتكون صفرًا (بناءً على اختبار ذي وجهين عادةً).

ثانيًا: استخدام 95%CI وهامش الخطأ المطلوب (هامش الخطأ = نصف 95%CI). تكمن مشكلة تحديد الهامش في أن هامش 5% يختلف عندما نقدر نسبة 50% أو 70% ويختلف عند تقدير نسبة 20%.

نتائج النهج الأول:

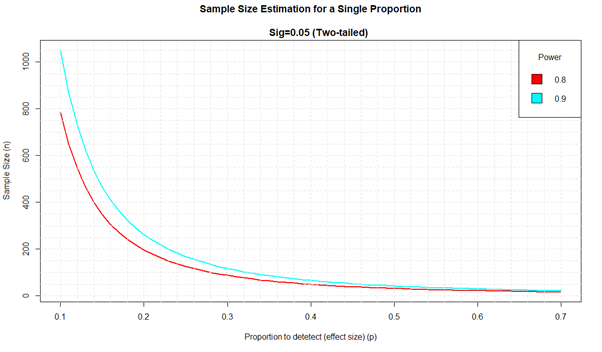
هذا ما حصلنا عليه نتيجة المحاكاة لقيم مختلفة من القوة وحجم التأثير للنهج الأول.

لذلك على سبيل المثال لتقدير نسبة 0.2 ، نحتاج إلى n = 263 لجانبين 95%CI والطاقة 0.9.

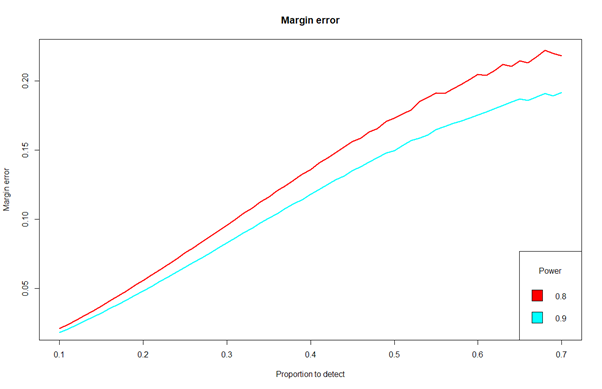
لاحظ أنه بالنسبة لهذه الطريقة ، لم يتم إصلاح هامش الخطأ لـ 95%CI (والذي لا يعرفه بعض الأشخاص بشكل واضح). ينمو مع النسبة المقدرة (انظر الرسم البياني الثاني أدناه) وهو أمر منطقي لأننا لا نحتاج إلى هامش 5% لتقدير النسبة 70% (عادة). بالنسبة لـ 70% ، لدينا هامش يبلغ حوالي 20% وهو ما يمكن مقارنته بامتلاك هامش 5% مقابل نسبة 20% أقل.

لذلك بالنسبة لمثالنا مع نسبة 20% لتقدير الطريقة الأولى ، ستعطينا خطأ هامش يبلغ 4.83% بالضبط. بعبارة أخرى ، لتقدير الحد الأدنى للنسبة المتوقعة البالغة 0.2 مع هامش الخطأ 4.83% باستخدام 95%CI ، نحتاج إلى 263 مريضًا.

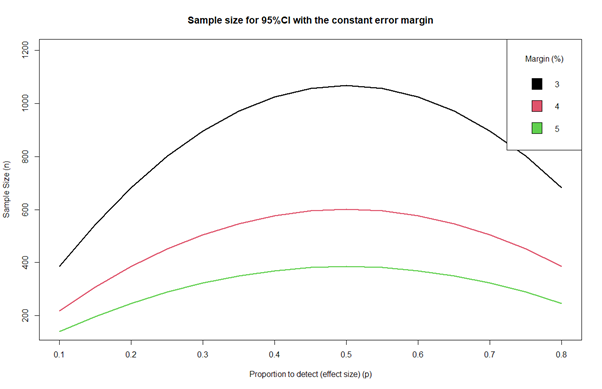
النهج الثاني يقوم على إصلاح خطأ الهامش (الحبكة الثالثة). كما يمكنك أن ترى أن وظيفة حجم العينة في هذه الحالة لها دائمًا حد أقصى عند p = 0.50. لذلك ، إذا كنت تريد إصلاح الهامش ، يمكنك اختيار الحد الأقصى n باعتباره أسوأ سيناريو.

يأتي التناقض بين هاتين الطريقتين من حقيقة أنه في النهج الأول ، تم تقدير 95%CI بقدر ضيق كما هو مطلوب لرفض الفرضية الصفرية. من خلال طلب هامش أصغر في الطريقة الثانية ، فإنك تدفع ثمن حجم العينة الأكبر ولكن دقة تقدير أفضل.

أي طريقة تختار؟ هذا يعتمد على هدفك. إذا كنت بحاجة إلى عينة أصغر ، فاختر الطريقة الأولى ولكن كن على دراية بهامش الخطأ. إذا كنت بحاجة إلى تصنيف أفضل ويمكنك جمع المزيد من الأفراد ، فإن الطريقة الثانية هي الطريقة الأفضل.